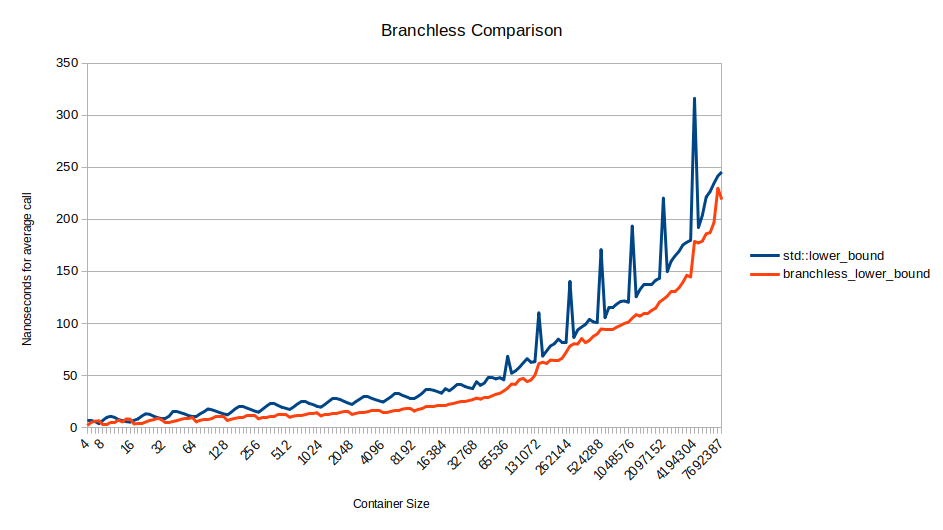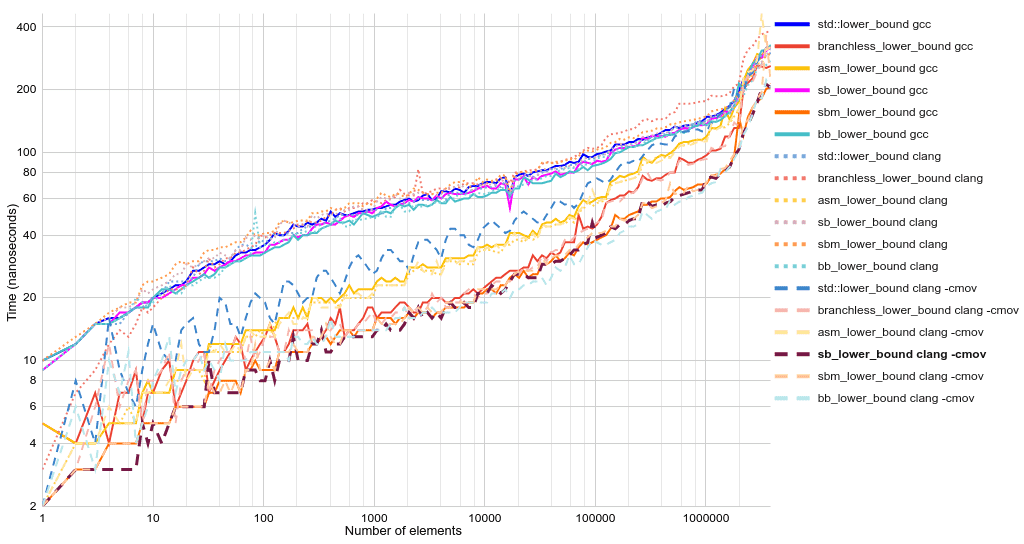
Мои читатели — занятые люди, поэтому сразу перейду к делу. Вот она, самая быстрая обобщённая (и простая) реализация двоичного поиска на C++:
template <class ForwardIt, class T, class Compare>
constexpr ForwardIt sb_lower_bound(
ForwardIt first, ForwardIt last, const T& value, Compare comp) {
auto length = last - first;
while (length > 0) {
auto rem = length % 2;
length /= 2;
if (comp(first[length], value)) {
first += length + rem;
}
}
return first;
}
Тот же интерфейс функции, что и у std::lower_bound, но вдвое быстрее и короче. «Без ветвления», потому что if компилируется в команду условной передачи, а не в ветвление/условный переход. Ближе к концу статьи мы изучим опции компилятора и даже более быстрые версии полностью без ветвления. Для понимания этой статьи не нужны особые знания в C++. Достаточно понимать, что итераторы (first и last) по сути являются указателями на элементы массива, хотя могут указывать на один элемент дальше, чем последний элемент массива. Можете не обращать внимания на template, class, constexpr и &. Вот если бы существовал быстрый и чистый язык, работающий на уровне железа...1 2Читать полностью »