Некоторые задачи школьной математики. Часть II

в 6:35, , рубрики: Занимательные задачки, математика, метод оценок, модули

Часть I. Дроби
Часть II. Модули

В данной статье рассматривается метод оценок диапазона принимаемых значений и связь этого метода с задачами, содержащими модуль.

При решении некоторых задач необходимо рассматривать диапазон, в пределах которого может находиться искомая величина.

Рассмотрим метод оценок при решении неравенств.

Предположим, что цена за одну единицу товара может колебаться в пределах от 5 до 10 RUB. Дать оценку сверху означает определить максимальное значение, которое может принимать искомая величина. Для двух единиц товара, цена за который не превышает 10 оценка сверху составит 10+10=20.

Рассмотрим задачу из задачника профильной направленности М.И. Башмакова
37. Известны оценки для переменных $ x $ и $ y: 0<x<5, 2<y<3.$

Дайте оценки сверху для следующих выражений:
1. $ 2x+3y $
2. $ xy $

Указание к решению задач 5 и 6

Для оценки дробных выражений необходимо воспользоваться следующим свойством числовых неравенств:
  • Если $a<b$ и оба числа положительны, то $ frac{ 1 }{a}>frac{ 1 }{b}$

5. $ frac{ 1 }{y} $
6. $ frac{ x }{y} $

8. $ x-y $
9. $ 3x-2y $

Ответы

1. $ 2x+3y<19 $
5. $ frac{ 1 }{y} < frac{ 1 }{2} $
9. $ 3x-2y<11 $


Вообще, анализ бесконечно малых величин использует критерий оценки. Понятие модуля как окрестности лежит в самом определении предела.

$ left|x_{n}-aright|<varepsilon $

Рассмотрим пример из «Курса дифференциального и интегрального исчисления» 363(6)

Легко установить расходимость ряда

$ sum frac{ 1 }{sqrt{n} }=1+frac{ 1 }{sqrt{2}}+ frac{ 1 }{sqrt{3}} + ... + frac{ 1 }{sqrt{n}} + ... $

В самом деле, так как члены его убывают, то n-я частичная сумма

$ 1+frac{ 1 }{sqrt{2}}+...+ frac{ 1 }{sqrt{n}}>ncdotfrac{ 1 }{sqrt{n}}=sqrt{n} $

и растёт до бесконечности вместе с $ n $.

Для того, чтобы доказать, что $ 1+frac{ 1 }{sqrt{2}}+...+ frac{ 1 }{sqrt{n}} $ действительно больше $ sqrt{n} $, нужно произвести оценку снизу данного выражения. Получим систему неравенств

$ left{!begin{aligned} & frac{ 1 }{sqrt{n-1}} > frac{ 1 }{sqrt{n}} \ & frac{ 1 }{sqrt{n-2}} > frac{ 1 }{sqrt{n}} \ & frac{ 1 }{sqrt{n-3}} > frac{ 1 }{sqrt{n}} \ & ... end{aligned}right. $

Произведя сложение всех неравенств данной системы, получим

$ 1+frac{ 1 }{sqrt{2}}+ frac{ 1 }{sqrt{3}} + ... + frac{ 1 }{sqrt{n}} > frac{ 1 }{sqrt{n}} +frac{ 1 }{sqrt{n}} + frac{ 1 }{sqrt{n}} +...+ frac{ 1 }{sqrt{n}}=ncdotfrac{ 1 }{sqrt{n}} $

Что и требовалось

С гармоническим рядом такой прием не проходит, потому что $ n $-я частичная сумма гармонического ряда

$ 1+frac{ 1 }{2}+ frac{ 1 }{3} + ... + frac{ 1 }{n} > ncdotfrac{ 1 }{n}=1 $

Вернёмся к задаче

38. Вычислить сумму ( «Задачи для детей от 5 до 15 лет»)

$frac{ 1 }{ 1cdot2 } + frac{ 1 }{ 2cdot3 } + frac{ 1 }{ 3cdot4 } + ... + frac{ 1 }{ 99cdot100 }$

(с ошибкой не более 1% от ответа)

Оценка сверху суммы ряда $ frac{ n }{ n+1 } $ даёт число 1.

Отбросим первое слагаемое $ frac{ 1 }{ 1cdot2 } $ 

(define series_sum_1
 ( lambda (n)
  (if (= n 0) 0 
    (+ (/ 1.0 (* (+ n 1.0 )(+ n 2.0))) (series_sum_1(- n 1.0)))
  ) ) )
(writeln (series_sum_1 10))
(writeln (series_sum_1 100))
(writeln (series_sum_1 1000))
(writeln (series_sum_1 10000))
(writeln (series_sum_1 100000))
(writeln (series_sum_1 1000000))

Получим $ 1 - frac{ 1 }{ 1cdot2 }=frac{ 1 }{ 2} $
0.41666666666666663
0.49019607843137253
0.4990019960079833
0.4999000199960005
0.49999000019998724
0.4999990000019941

Проверить можно в ideone.com здесь

Этот же алгоритм на Python

def series_sum(n):
	if n==0:
		return 0
	else:
		return 1.0/((n+1.0)*(n+2.0))+series_sum(n-1.0)
 
print(series_sum(10))
print(series_sum(100))

Ссылка на ideone.com

Отбросим два первых слагаемых $ frac{ 1 }{ 1cdot2 } + frac{ 1 }{ 2cdot3 } $ 

(define series_sum_1
 ( lambda (n)
  (if (= n 0) 0 
    (+ (/ 1.0 (* (+ n 2.0) (+ n 3.0))) (series_sum_1(- n 1.0)))
  ) ) )
(series_sum_1 1000000)

Получим 0.33333233333632745

Положительный ряд всегда имеет сумму; эта сумма будет конечной (и, следовательно, ряд — сходящимся), если частичные суммы ряда ограничены сверху, и бесконечной (а ряд — расходящимся) в противном случае.

Подсчитаем сумму гармонического ряда при увеличении $ n $

#lang racket
(define series_sum_1
 ( lambda (n)
  (if (= n 0) 0 
    (+ (/ 1.0 n) (series_sum_1(- n 1.0)))
  ) ) )
(series_sum_1 10)
(series_sum_1 100)
(series_sum_1 1000)
(series_sum_1 10000)
(series_sum_1 100000)
(series_sum_1 1000000)

Получим:

2.9289682539682538
5.187377517639621
7.485470860550343
9.787606036044348
12.090146129863335
14.392726722864989

Если отбросить много (но не бесконечно много) начальных слагаемых, то сумма ряда также будет увеличиваться (и стремиться к $ infty $) при увеличении $ n $.
Частичные суммы нарастают безгранично — ряд расходится.

Решите задачу («Начала теории множеств»):

Бизнесмен заключил с чёртом сделку: каждый день он даёт чёрту одну монету, и в обмен получает любой набор монет по своему выбору, но все эти монеты меньшего достоинства (видов монет конечное число). Менять (или получать) деньги в другом месте бизнесмен не может. Когда монет больше не останется, бизнесмен проигрывает.

Докажите, что рано или поздно чёрт выиграет, каков бы ни был начальный набор монет у бизнесмена.

Вернёмся к модулям.
В интегральном исчислении модуль используется в формуле

$ int frac{1}{x} dx=int frac{dx}{x}=ln left| x right| + C $

На Хабре была статья Самый натуральный логарифм, в которой рассматривается этот интеграл и на основе его вычисление числа $ e $. Напишите, пожалуйста, в комментах как вообще работает эта программа и зачем нужен пустой дефайн вроде " #define o "

Присутствие модуля в формуле $ int frac{dx}{x}=ln left| x right| + C $ обосновывается далее в «Курсе дифференциального и интегрального исчисления»

Если… $ x < 0 $, то дифференцированием легко убедиться в том, что $ left[ ln (-x) right]'=frac{1}{x} $

Физическое приложение интеграла $ int frac{dx}{x} $

Этот интеграл используется для вычисления разности потенциалов обкладок цилиндрического конденсатора.

Некоторые задачи школьной математики. Часть II - 38

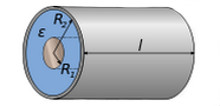
«Электричество и магнетизм»:

Разность потенциалов между обкладками находим путем интегрирования:

$ varphi_{1}- varphi_{2}=intlimits_{R_{1}}^{R_{2}} E(r) dr=frac{q}{2 pi varepsilon_{0} varepsilon l} intlimits_{R_{1}}^{R_{2}} frac{dr}{r}=frac{q}{2 pi varepsilon_{0} varepsilon l} ln frac{R_{2}}{R_{1}} $

( $ R_{1} $ и $R_{2} $ — радиусы внутренней и внешней обкладок).

Здесь не используется знак модуля под знаком натурального логарифма $ ln left| frac{R_{2}}{R_{1}} right| $, потому что $ R_{1} $ и $R_{2} $ строго положительны и такая форма записи является избыточной.

«Модульное» рисование

С помощью модулей можно рисовать различные фигуры.

Если в программе geogebra написать формулу $ abs(x)+abs(y)=1 $ получим

Некоторые задачи школьной математики. Часть II - 46

Можно рисовать более сложные фигуры. Нарисуем, например, «бабочку» в облаке WolframAlpha

$ sum frac{ left| x right| }{n-left| x right| }+ frac{ left| x+n right| }{n} + frac{ left| x-n right| }{n} $

Некоторые задачи школьной математики. Часть II - 48

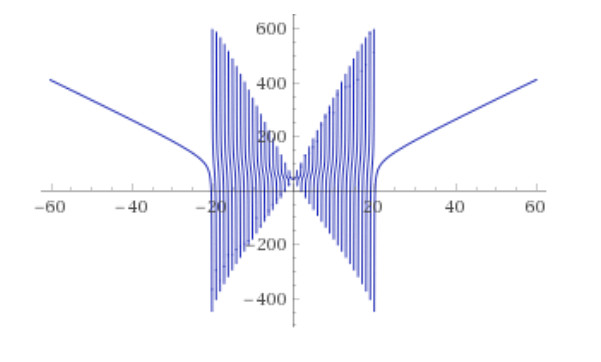
ссылка на рисунок

Книги:

«Задачник профильной направленности» М.И. Башмаков
«Начала теории множеств» Н.К. Верещагин, А. Шень
Курс общей физики: в 3-х т. Т. 2. «Электричество и магнетизм» И.В. Савельев

Автор: Дмитрий

Источник

* - обязательные к заполнению поля

Главная   |  Архив новостей  |   Android  |   Google  |   Apple  |   Microsoft  |   Информационная безопасность  |   Веб – разработка
Публикации RSS  |  Комментарии RSS
https://ajax.googleapis.com/ajax/libs/jquery/3.4.1/jquery.min.js