Карл Фридрих Гаусс
Математик и историк математики Джереми Грей рассказывает Гауссе и его огромном вкладе в науку, о теории квадратичных форм, открытии Цереры, и неевклидову геометрию*

Портрет Гаусса Эдуарда Ритмюллера на террасе обсерватории Геттингена // Карл Фридрих Гаусс: Титан науки Г. Уолдо Даннингтона, Джереми Грея, Фриц-Эгберт Дохе
Карл Фридрих Гаусс был немецким математиком и астрономом. Он родился у бедных родителей в Брауншвейге в 1777 году и скончался в Геттингене в Германии в 1855 году, и к тому времени все, кто его знал, считали его одним из величайших математиков всех времен.
Изучение Гаусса
Как мы изучаем Карла Фридриха Гаусса? Ну, когда дело доходит до его ранней жизни, мы должны полагаться на семейные истории, которыми поделилась его мать, когда он стал знаменитым. Конечно, эти истории склонны к преувеличению, но его замечательный талант был заметен, уже когда Гаусс был в раннем подростковом возрасте. С тех пор у нас появляется все больше записей о его жизни.
Когда Гаусс вырос и стал замечен, у нас начали появляться письма о нем людьми, которые его знали, а также официальными отчетами разного рода. У нас также есть длинная биография его друга, написанная на основе бесед, которые они имели в конце жизни Гаусса. У нас есть его публикации, у нас очень много его писем к другим людям, и много материала он написал, но так и не опубликовал. И, наконец, у нас есть некрологи.
Ранняя жизнь и путь к математике
Отец Гаусса занимался различными делами, был рабочим, мастером строительной площадки и купеческим ассистентом. Его мать была умной, но едва грамотной, и посвятила всю себя Гауссу до самой своей смерти в возрасте 97 лет. Похоже, что Гаусс был замечен как одаренный ученик еще в школе, в одиннадцать лет, его отца убедили отправить его в местную академическую школу, вместо того, чтобы заставить его работать. В то время Герцог Брауншвейгский стремился модернизировать своё герцогство, и привлекал талантливых людей, которые бы помогли ему в этом. Когда Гауссу исполнилось пятнадцать, герцог привел его в коллегию Каролинум для получения им высшего образования, хотя к тому времени Гаусс уже самостоятельно изучил латынь и математику на уровне высшей школы. В возрасте восемнадцати лет он поступил в Геттингенский университет, а в двадцать один уже написал докторскую диссертацию.
Первоначально Гаусс собирался изучать филологию, приоритетный предмет в Германии того времени, но он также проводил обширные исследования по алгебраическому построению правильных многоугольников. В связи с тем, что вершины правильного многоугольника из N сторон задаются решением уравнения $inline$x^{(n – 1)} = 0$inline$ (что численно равно $inline$e^{(2ki pi/17)} = cos(2k pi/17) + i sin(2k pi/17), k =0, 1, . . . 16)$inline$. Гаусс обнаружил, что при n = 17 уравнение факторизуется таким образом, что правильный 17-сторонний многоугольник может быть построен только по линейке и циркуля. Это был совершенно новый результат, греческие геометры не подозревали об этом, и открытие вызвало небольшую сенсацию — новости об этом даже были опубликованы в городской газете. Этот успех, который пришел, когда ему едва исполнилось девятнадцать, заставил его принять решение изучать математику.
Но то, что сделало его знаменитым, было два совершенно разных явления в 1801 году. Первым было издание его книги под названием «Арифметические рассуждения», которая полностью переписала теорию чисел и привела к тому, что она( теория чисел) стала, и до сих пор является, одним из центральных предметов математики. Она включает в себя теорию уравнений вида x ^ n — 1, являющейся одновременно очень оригинальной и в то же время легко воспринимаемой, а также гораздо более сложную теорию, называемую теорией квадратичной формой. Это уже привлекло внимание двух ведущих французских математиков, Джозефа Луи Лагранжа и Адриена Мари Лежандра, которые признали, что Гаусс ушел очень далеко за пределы всего того, что они делали.
Вторым важным событием было повторное открытие Гауссом первого известного астероида. Он был найден в 1800 году итальянским астрономом Джузеппе Пьяцци, который назвал его Церерой в честь римской богини земледелия. Он наблюдал ее в течение 41 ночи, прежде чем она исчезла за солнцем. Это было очень захватывающее открытие, и астрономы очень хотели знать, где он появится снова. Только Гаусс рассчитал это правильно, чего не сделал никто из профессионалов, и это сделало его имя как астронома, которым он и остался на многие годы вперед.
Поздняя жизнь и семья
Первая работа Гаусса была математиком в Геттингене, но после открытия Цереры, а затем и других астероидов он постепенно переключил свои интересы на астрономию, а в 1897 году стал директором Геттингенской обсерватории, и занимал эту должность почти до самой смерти. Он также оставался профессором математики в Геттингенском университете, но это, похоже, не требовало от него большого преподавания, а записи о его контактах с молодыми поколениями была довольно незначительной. Фактически, он, кажется, был отчужденной фигурой, более комфортной и общительной с астрономами, и немногими хорошими математиками в его жизни.
В 1820-х годах он руководил массированным исследованием северной Германии и южной Дании и в ходе этого переписывал теорию геометрии поверхностей или дифференциальную геометрию, как ее называют сегодня.
Гаусс женился дважды, в первый раз довольно счастливо, но когда его жена Джоанна умерла во время родов в 1809 году, он снова женился на Минне Вальдек, но этот брак оказался менее успешным; Она умерла в 1831 году. У него было трое сыновей, двое из которых эмигрировали в Соединенные Штаты, скорее всего, потому что их отношения с отцом были проблемными. В результате в Штатах существует активная группа людей, которые ведут свое происхождение от Гаусса. У него также было две дочери, по одной от каждого брака.
Величайший вклад в математику
Рассматривая вклад Гаусса в этой области, мы можем начать с метода наименьших квадратов в статистике, который он изобрел, чтобы понять данные Пьяцци и найти астероид Церера. Это был прорыв в усреднении большого количества наблюдений, все из которых были немного не точными, чтобы получить из них наиболее достоверную информацию. Что касается теории чисел, говорить об этом можно очень долго, но он сделал замечательные открытия о том, какие числа могут быть выражены квадратичными формами, которые являются выражениями вида $inline$3x^2 + 5xy + 6y^2$inline$. Вам может казаться, что это важно, но Гаусс превратил то, что было собранием разрозненных результатов в систематическую теорию, и показал, что многие простые и естественные гипотезы имеют доказательства, которые лежат в том, что похоже на другие разделы математики вообще. Некоторые приемы, которые он изобрел, оказались важными и в других областях математики, но Гаусс обнаружил их еще до того, как эти ветви были правильно изучены: теория групп — пример.
Его работа по уравнениям вида $inline$x ^{(n - 1)} = 0$inline$ и, что более удивительно, по глубоким особенностям теории квадратичных форм, открыла использование комплексных чисел, например, для доказательства результатов о целых числах. Это говорит о том, что многое происходило под поверхностью предмета.
Позже, в 1820-х годах, он обнаружил, что существует концепция кривизны поверхности, которая является неотъемлемой частью поверхности. Это объясняет, почему некоторые поверхности не могут быть точно скопированы на другие, без преобразований, как мы не можем сделать точную карту Земли на листе бумаги. Это освободило изучение поверхностей от изучения твердых тел: у вас может быть яблочная кожура, без необходимости представления яблока под ней.
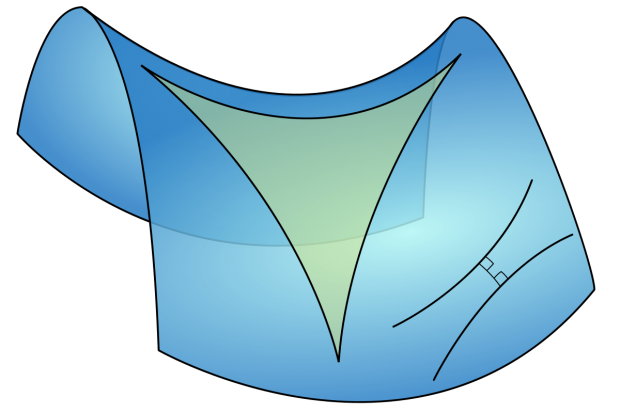
Поверхность с отрицательной кривизной, где сумма углов треугольника меньше, чем у треугольника на плоскости //source:Wikipedia
В 1840-х годах, независимо от английского математика Джорджа Грина, он изобрел предмет теории потенциала, который является огромным расширением исчисления функций нескольких переменных. Это правильная математика для изучения гравитации и электромагнетизма и с тех пор используется во многих областях прикладной математики.
И мы также должны помнить, что Гаусс открыл, но не опубликовал довольно много. Никто не знает, почему он так много сделал для себя, но одна теория состоит в том, что поток новых идей, которые он держал в голове был еще более захватывающим. Он убедил себя в том, что геометрия Евклида не обязательно истинна и что по крайней мере одна другая геометрия логически возможна. Слава этому открытию досталась двум другим математикам, Бойяю в Румынии-Венгрии и Лобачевскому в России, но только после их смерти — настолько это было спорно в то время. И он много работал над так называемыми эллиптическими функциями — вы можете рассматривать их как обобщения синусоидальных и косинусных функций тригонометрии, но, если более точно, они являются сложными функциями комплексной переменной, а Гаусс изобрел целую теорию из них. Десять лет спустя Абель и Якоби прославились тем, что сделали то же самое, не зная, что это уже сделал Гаусс.
Работа в других областях
После своего повторного открытия первого астероида, Гаусс много работал над поиском других астероидов и вычислением их орбит. Это была трудная работа в докомпьютерную эпоху, но он обратился к своим талантам, и он, похоже, почувствовал, что это работа позволила ему выплатить свой долг принцу и обществу, которое дало ему образование.
Кроме того, во время съемки в северной Германии он изобрел гелиотроп для точной съемки, а в 1840-х годах он помог создать и построить первый электрический телеграф. Если бы он также подумал об усилителях, он мог бы отметиться и в этом, так как без них сигналы не могли путешествовать очень далеко.
Прочное Наследие
Есть много причин, почему Карл Фридрих Гаусс по-прежнему так актуален сегодня. Прежде всего, теория чисел превратилась в огромный предмет с репутацией очень сложного. С тех пор некоторые из лучших математиков тяготеют к нему, и Гаусс дал им способ приблизиться к нему. Естественно, некоторые проблемы, которые он не смог решить, привлекли к себе внимание, поэтому вы можете сказать, что он создал целую область исследований. Оказывается, у этого также есть глубокие связи с теорией эллиптических функций.
Кроме того, его открытие внутренней концепции кривизны обогатило все изучение поверхностей и вдохновило на многие годы работы последующие поколения. Любой, кто изучает поверхности, от предприимчивых современных архитекторов до математиков, находится у него в долгу.
Внутренняя геометрия поверхностей простирается до идеи внутренней геометрии объектов более высокого порядка, таких как трехмерное пространство и четырехмерное пространство-время.
Общая теория относительности Эйнштейна и вся современная космология, в том числе изучение черных дыр, стали возможными благодаря тому, что Гаусс совершил этот прорыв. Идея неевклидовой геометрии, столь шокировавшая в свое время, заставляла людей осознавать, что может быть много видов строгой математики, некоторые из которых могут быть более точными или полезными — или просто интересными -, чем те, о которых мы знали.
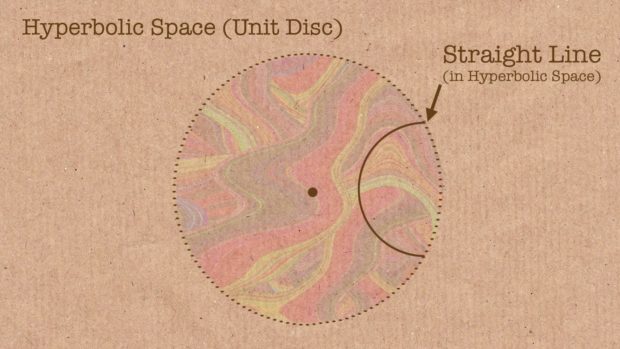
Неевклидова геометрия // источник: Numberphile
Человек за легендой
Жизнь Гаусса породила много историй и анекдотов. Например, как ни невероятно, его мать любила говорить, что никто не преподавал основы арифметики Гауссу, но он сам справился с ней, слушая своего отца на работе. Несомненно, он был одним из немногих математиков с необычайной способностью к умственной арифметике и мог быстро и аккуратно проводить длинные вычисления в уме. Также сообщалось, что его сыновья говорили, что он отговаривал их от продолжения карьеры в науке, потому что «он не хотел, чтобы имя Гаусса ассоциировалось со второсортной работой».
В том же духе у него была пугающая привычка говорить людям, что он уже знал то, что они только что обнаружили. Наиболее известный случай, когда его старый университетский друг Фаркаш Бойаи написал ему, приложив копию открытия своего сына Яноса неевклидовой геометрии, Гаусс ответил, что он не может похвалить работу, заявив — «потому, что делать это все равно, что хвалить себя». Это не только преувеличивало то, что знал Гаусс в 1831 году, он и не сделал ничего, чтобы помочь молодому Бойи получить признание за его работу, и Янош настолько разочаровался, что больше никогда не публиковал его.
Однако у вас не должно создаться впечатления, что Гаусс был неприятным человеком. Он был принципиальным человеком, он был счастлив принять Софи Жермен как серьезного математика в то время, когда женщины были исключены из высшего образования, и он всегда стремился использовать свои таланты для продуктивного использования. Но его исключительные таланты, и, хотя мы можем только порадоваться за них, Радакторвероятно, сделали его очень одиноким.
Джереми Грей, доктор, заслуженный пр.фессор истории математики, Открытый университет.
* Неточный перевод.
Автор: Koka77








