Здравствуйте!
Расскажу о серии задач, которая случайно возникла в процессе решения другой задачи. Мне на глаза попалось равенство:
81 * 27 = 2187
– Интересно, – подумал я. – А бывают ли ещё такие числа, чтобы цифры слева и справа повторялись?
Всего нашлось 7 двузначных пар, включая одну с теми же цифрами:
15 * 93 = 1395
21 * 60 = 1260
21 * 87 = 1827
27 * 81 = 2187
30 * 51 = 1530
35 * 41 = 1435
80 * 86 = 6880
Затем я решил посчитать, сколько пар n-значных чисел удовлетворяют этому свойству: набор цифр и количество повторений каждой из них слева и справа от знака "равно" совпадают. Заметим, что произведение двух n-значных чисел может иметь как 2n-1, так и 2n знаков. (Можно вычислить, что доля пар n-значных чисел, для которых в произведении 2n знаков составляет примерно 82,7%).
Для небольших значений n я получил результат с помощью программы на Питоне. Алгоритм очень простой - берём все пары чисел, переводим в десятичное представление и сравниваем наборы цифр в паре чисел и в их произведении. На вычисление количества пар для n=5 ушло более 3 часов. Переписав на С++, на вычисление ушло 25 минут, но т.к. следующее значение требует рассмотрение в 100 раз больше пар, то ждать так долго не хотелось.
|
n |
количество интересных пар |
|
1 |
0 |
|
2 |
7 |
|
3 |
156 |
|
4 |
3399 |
|
5 |
112025 |
|
6 |
4505706 |
Задумавшись о том, можно ли посчитать количество таких пар для бóльших чисел n, я придумал усовершенствованный алгоритм, который позволил получить значение для n=6: 4505706 за 62 минуты. Для n больше 6 уже требуется очень много памяти.
Если нанести полученные значения на график, получим вот такую картинку:
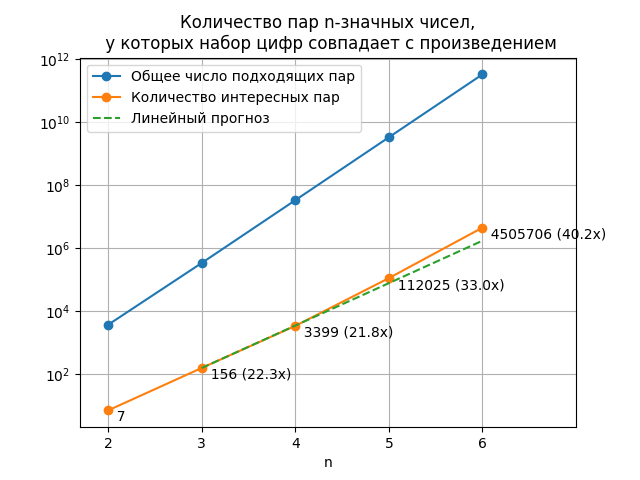
Было бы любопытно узнать, как график ведёт себя на бесконечности, — вероятно, есть какая-то асимптота.
Потом я задумался, а какие из всех этих чисел наиболее интересные. Например, существуют ли пары одинаковых чисел, обладающие описанным выше свойством. Оказывается, для n=5 и n=6 существуют:
72576 * 72576 = 5267275776
406512 * 406512 = 165252006144
415278 * 415278 = 172455817284
494462 * 494462 = 244492669444
603297 * 603297 = 363967270209
725760 * 725760 = 526727577600
Также возник вопрос, а может ли быть что-то вроде abc*def = abcdef. Очевидный ответ: нет, поскольку def должно в данном случае превышать 1000 (делим правую часть на abc).
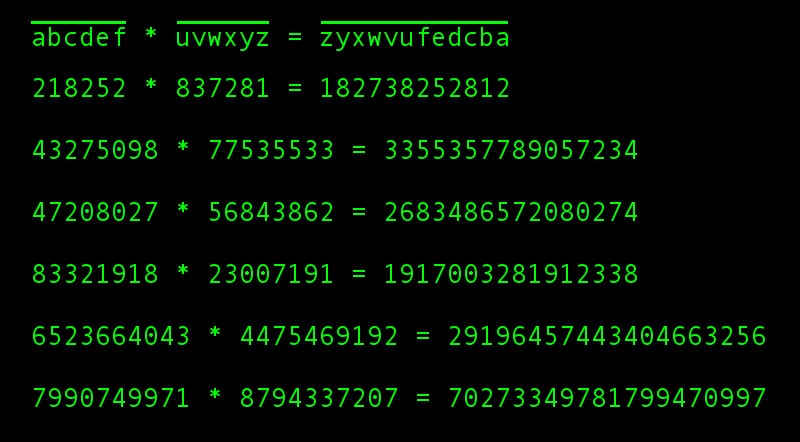
Тогда резонный вопрос, а может ли быть что-то вроде abc*def = fedcba, то есть в произведении цифры идут в обратном порядке. (Отметим, что в данном случае порядок множителей имеет значение.) Будем называть такие числа переворачивающимися парами.
И оказывается, да! Такие случаи бывают.
При n < 6 – нет пар
n=6
218252 * 837281 = 182738252812
По этому поводу я придумал алгоритм побыстрее для решения конкретно этой задачи.
n=7 – нет пар
n=8
43275098 * 77535533 = 3355357789057234
47208027 * 56843862 = 2683486572080274
83321918 * 23007191 = 1917003281912338
n=9 – нет пар
n=10
6523664043 * 4475469192 = 29196457443404663256
7990749971 * 8794337207 = 70273349781799470997
n=11 – нет пар
n=12 - нет пар (вычисления длились 5 часов на 11-ядрах процессора)
Видна одна закономерность: для нечётных n не нашлось ни одной пары. Интересно, таких пар вообще не существует, или просто их число существенно меньше.
Неудачная идея доказательства
У меня было подозрение, что это как-то связано с признаком деления, например на 11: остаток от деления десятичного числа на 11 равен остатку от деления на 11 знакопеременной суммы цифр. Для чётных n и переворачивающейся пары с остатками от деления на 11 (x, y) получаем:
x*y mod 11 = (x+y) mod 11
Для нечётных n получаем:
x*y mod 11 = (x-y) mod 11
Однако эти равенства приводят к одинаковому количеству пар остатков от деления на 11 - по 10 пар (из 121 варианта) для чётных и нечётных n.
Кстати, из признака деления на 3 получаем, что x mod 3 != 1 и y mod 3 != 1.
Признак деления на 9 отсекает ещё часть вариантов - реализуются 6 из 81 варианта.
Другие системы счисления
Если посмотреть на системы счисления с другими основаниями M, то в некоторых из них существуют переворачивающиеся пары для нечётных n.
Hidden text
(Поиск пар производился для указанных n)
M=2
n<27 нет пар
n=27
111101110000100111010111111 * 100100001010111100111010001 = 100010111001111010100001001111111010111001000011101111
M=3
n<17 нет пар
n=17
21111012220201202 * 20212211222110221 = 1220112221122120220210202221011112
n=18
n=19
n=20
M=4
n=2
n=3
n=4
2211 * 3102 = 20131122
n=5
n=6
330113 * 122021 = 120221311033
n=7
n=8
n=9
M=5
n=1
n=2
n=3
n=4
n=5
22231 * 43412 = 2143413222
n=6
303424 * 311102 = 201113424303
n=7
n=8
n=9
M=6
n=2
n=3
n=4
n=5
40204 * 13001 = 1003140204
n=6
n=7
n=8
n=9
M=7
n=2
42 * 42 = 2424 (в десятичной системе соответствует 30*30=900)
n=3
n=4
n=5
n=6
n=7
n=8
46343406 * 46631433 = 3341366460434364
65305023 * 26140452 = 2540416232050356
n=9
M=8
n=2
n=3
n=4
6352 * 4023 = 32042536
n=5
n=6
552435 * 166321 = 123661534255
n=7
6037502 * 4000203 = 30200042057306
n=8
41250414 * 27061041 = 1401607241405214
n=9
554442365 * 175010131 = 131010571563244455
M=9
n=2
n=3
n=4
n=5
n=6
444572 * 480042 = 240084275444
n=7
n=8
n=9
M=10
n=2
n=3
n=4
n=5
n=6
218252 * 837281 = 182738252812
n=7
n=8
43275098 * 77535533 = 3355357789057234
47208027 * 56843862 = 2683486572080274
83321918 * 23007191 = 1917003281912338
n=9
M=11
n=2
n=3
n=4
n=5
n=6
n=7
n=8
n=9
54AA50055 * 246902221 = 12220964255005AA45
M=12
n=2
n=3
n=4
4718 * 5A22 = 22A58174
6596 * 9A35 = 53A96956
n=5
80408 * 16001 = 1006180408
90309 * 14001 = 1004190309
n=6
n=7
3B0B9B3 * 5418B81 = 18B81453B9B0B3
n=8
79BB17A7 * 22862551 = 155268227A71BB97
n=9
M=13
n=2
n=3
n=4
n=5
n=6
n=7
n=8
n=9
M=14
n=2
n=3
n=4
n=5
n=6
n=7
CA94B86 * 29D2862 = 2682D9268B49AC
n=8
n=9
Также интересны случаи, когда в левой и правой части каждая цифра используется по 1 разу. И наиболее замечательны случаи, когда все цифры от 0 до 9 используются (n=5). Таких случаев я насчитал 1289. Будем называть такие числа полными парами.
Было бы интересно найти пару чисел, пусть даже не в десятичной системе счисления, которая одновременно является переворачивающейся и полной. (В случае системы счисления с основанием M, при n=M/2, в паре чисел и в произведении все “цифры” от 0 до M-1 должны встретиться по 1 разу.). Кажется, что таких пар вообще не существует. Ведь примерная вероятность оценивается в {число переворачивающихся пар} * {число полных пар} / {число потенциальных пар}2, что при M=12 (n=6) оценивается порядка 5*10-20 при условии наличия одной переворачивающейся пары (в реальности таких пар не нашлось). И вроде как эта вероятность с ростом M убывает, поэтому, возможно, таких пар вообще не существует.
Кстати, если искать пары чисел состоящих из различного числа цифр, то одну переворачивающуюся полную пару я всё-таки нашёл:
5 * 20341 = 143025 (система счисления с основанием M=6)
Всё выше изложенное жёстко связано с системой счисления, поэтому не представляет настолько большого интереса, как глобальные задачи теории чисел, такие как проблема Гольдбаха, гипотеза Каталана, теорема Лежандра о сумме четырёх квадратов, гипотеза о разложении в сумму трёх кубов и др. Хотя кто знает, может быть какое-то практическое применение, кроме ребусов, всё же найдётся.
P. S. Если нужно, код выложу чуть позже.
UPDATE
Код на Питоне для исходной задачи
Hidden text
for n in range(1, 4+1):
p = 10**(n-1)
count = 0
for i in range(p, p*10):
for j in range(i, p*10):
if sorted(str(i)+str(j)) == sorted(str(i*j)):
count += 1
print(n, count)Код на Питоне для поиска переворачивающихся пар
Hidden text
MIN = 1
MAX = 8
divisors_mod10 = [[[] for j in range(10)] for i in range(10)]
for i in range(10):
for j in range(10):
divisors_mod10[(i*j)%10][i].append(j)
def f(i, si, n, k, sj, accum):
if k == n:
if sj[0] >= sj[n-1]:
j = int("".join(map(str, sj)))
sm = "".join(map(str, (si + sj)[::-1]))
if int(sm) == i*j:
print(f"{i} * {j} = {sm}")
return
for k1 in range(k):
accum += si[n-1-k+k1]*sj[n-1-k1]
vd = divisors_mod10[(si[k] - (accum % 10) + 10) % 10][si[n-1]]
for divisor in vd:
sj[n-1-k] = divisor
if k == 0 and si[0] < sj[n-1]:
continue
f(i, si, n, k+1, sj, (accum + si[n-1]*sj[n-1-k])//10)
for n in range(MIN, MAX+1):
print(f"n={n}")
p = 10**(n-1)
for i in range(p+1, p*10):
if i % 3 == 1:
continue
if i % p == 0:
print(i)
si = list(map(int, str(i)))
sj = [0]*len(si)
f(i, si, n, 0, sj, 0);
Код на С/C++ для исходной задачи (для случая n=6)
Hidden text
#include <iostream>
#include <algorithm>
#include <vector>
#include <map>
#include <cstring>
using namespace std;
typedef long long LL;
typedef char T;
const int MAX = 6;
// Check if two histograms coincide
bool eq(T* h1, T* h2) {
for (int i=0; i<10; i++) {
if (h1[i] != h2[i]) {
return false;
}
}
return true;
}
// Convert a number to a histogram of its decimal digits
// Assuming h initialized with zeros
void get_histogram(LL x, T *h) {
while (x != 0) {
h[x % 10]++;
x /= 10;
}
}
// Add two histograms
void add(T *h1, T *h2) {
for (int i=0; i<10; i++) {
h1[i] += h2[i];
}
}
// Add two histograms
void add(T *h, T *h1, T *h2) {
for (int i=0; i<10; i++) {
h[i] = h1[i] + h2[i];
}
}
// Multiset difference
void subtract(T *h1, T *h2) {
for (int i=0; i<10; i++) {
if (h1[i] > h2[i]) {
h1[i] -= h2[i];
} else {
h1[i] = 0;
}
}
}
// Multiset inclusion: h1 >= h2
bool includes(T *h1, T *h2) {
for (int i=0; i<10; i++) {
if (h1[i] < h2[i]) {
return false;
}
}
return true;
}
// Encode histogram by a number (sorted multiset)
int to_number(T *h) {
int r = 1; // add leading 1
for (int i=0; i<10; i++) {
for (int j=0; j<h[i]; j++) {
r = r*10 + i;
}
}
return r;
}
// Decode number to a histogram
// Assuming h initialized with zeros
void from_number(int x, T *h) {
while (x > 1) {
h[x % 10]++;
x /= 10;
}
}
// Precompute histograms
void compute_histograms(int p, T *histograms) {
for (int i=p+1; i<p*10; i++) {
get_histogram(i, histograms + i*10);
}
}
// Precompute lists of integers that include a certain multiset of digits
void build_lists(int p, T *histograms, map<int, vector<int> > & lists) {
for (int x=1; x<=19999; x++) {
char sx[4+1+1];
sprintf(sx, "%d", x);
// Only consider valid "numbers"
if (sx[0] != '1') {
continue;
}
// Check if x is sorted
if (x > 1) {
bool sorted = true;
for (char *p=sx+1; *(p+1)!=0; p++) {
if (*p > *(p+1)) {
sorted = false;
break;
}
}
if (!sorted) {
continue;
}
}
T hx[10];
memset(hx, 0, 10*sizeof(T));
from_number(x, hx);
vector<int>& subnumbers = lists[x];
for (int i=p+1; i<p*10; i++) {
T * hi = histograms + i*10;
if (includes(hi, hx)) {
subnumbers.push_back(i);
}
}
}
}
int main() {
int p = 10*100;
for (int n = 4; n<=MAX; n++, p*=10) {
cout << "Computing histograms..." << endl;
T *histograms = new T[p*10*10];
memset(histograms, 0, 10*p*10*sizeof(T));
compute_histograms(p, histograms);
cout << "Building lists..." << endl;
map<int, vector<int> > lists;
build_lists(p, histograms, lists);
cout << "Counting..." << endl;
LL count = 0;
for (int i = p+1; i < p*10; i++) {
if (i % 10000 == 0) {
cout << i << endl;
}
auto hi = histograms + i*10;
int j_begin = max(i, static_cast<int>((static_cast<LL>(p)*p*10+i-1)/i));
LL ten_2n_minus_4 = static_cast<LL>(p)*p*100/10000;
while (j_begin < p*10) {
LL m = static_cast<LL>(i)*j_begin;
LL m_end = static_cast<LL>(m / ten_2n_minus_4 + 1)*ten_2n_minus_4;
int j_end = (m_end + i - 1) / i;
int first_digits = m / ten_2n_minus_4;
T hfd[10];
memset(hfd, 0, 10*sizeof(T));
get_histogram(first_digits, hfd);
subtract(hfd, hi);
vector<int> & subnumbers = lists[to_number(hfd)];
auto s_begin = lower_bound(subnumbers.begin(), subnumbers.end(), j_begin);
auto s_end = lower_bound(subnumbers.begin(), subnumbers.end(), j_end);
for (vector<int>::const_iterator it = s_begin; it != s_end; it++) {
int j = *it;
LL m2 = static_cast<LL>(i)*j;
if (m2 >= m_end) {
break;
}
T hm2[10];
memset(hm2, 0, 10*sizeof(T));
get_histogram(m2, hm2);
auto hj = histograms + 10*j;
for (int k=0; k<10; k++) {
if (hm2[k] != hi[k] + hj[k]) {
goto L;
}
}
count += 1;
L:
continue;
}
j_begin = j_end;
}
}
cout << n << " " << count << endl;
}
}
/*
4 3399
5 112025
6 4505706
*/Автор: Потапов Данила





