Продолжение серии статей, разбирающих идею суперскалярного процессора с
OoO и фронтендом стековой машины. Тема данной статьи — оптимизация обращений к памяти.
Предыдущие статьи:
1 — описание работы на линейном куске
2 — вызов функций, сохраняем регистры
3 — вызов функций, взгляд изнутри
До сих пор мы не обращали внимания на слабое место всех стековых машин — избыточные обращения к памяти.
В самом деле, когда наивный кодо-генератор стековой машины хочет получить значение переменной ‘a’, он пишет инструкцию ‘push a’. Возможностей сослаться на уже вычисленное выражение или его кусок стековый процессор не предоставляет.
Для регистровых процессоров компилятор решает эту проблему введением временных переменных с возможным размещением их в регистрах. Стоит придумать подобный механизм и для нашей внешне без-регистровой архитектуры.
Впрочем, придумывать то почти ничего и не надо, “всё уже украдено до нас”(С).
- введем аппарат закладок (bookmarks)
- закладка — регистр, к которому компилятор может обращаться по номеру, номера регистра и закладки совпадать не обязаны, хотя, это упростило бы жизнь
- компилятор для каждой функции определяет число закладок, которыми он собирается располагать
- при старте функции под закладки выделяется необходимое число регистров, освободить их нельзя вплоть до завершения функции
- закладки попадают внутрь регистрового окна и на них действует механизм FILL/SPILL
- если компилятор считает вычисленное значение ценным, то устанавливает закладку, например, инструкцией ‘bmk 1’, что означает: значение на вершине стека отныне считается закладкой с номером 1. Происходит ли при этом копирование значения в регистр закладки N1 или подменяется регистр, отвечающий за эту закладку, не важно, детали реализации
- когда в дальнейшем компилятору потребуется значение из этой закладки, он может его использовать, например, так: ‘add_bmk 1’, т.е. значение с вершины стека будет просуммировано со значением закладки 1 и замещено этим значением
- с точки зрения бэкенда процессора, будет порожден старый добрый моп суммирования двух регистров в третий
- возникает необходимость второй линейки арифметических и логических инструкций (add->add_bmk, mul->mull_bmk, cmp->cmp_bmk), но оно того стоит
- или более общий вариант — любой из аргументов или результат трех(двух)-адресной инструкции может быть закладкой
- можно себе представить и динамическое выделение закладок, без выделения максимального их количества в целях оптимизации количества использованных регистров, но это (на первый взгляд) выглядит слишком жестоким по отношению к железу
В результате у компилятора есть два условно новых ресурса для оптимизации.
Первый — выявление и размещение закладок, число которых может быть достаточно большим, оно не ограничено числом располагаемых регистров за отсутствием таковых. По большому счету это эквивалент локальных переменных, размещенных в “быстром” стеке.
Второй — эквивалентное преобразование выражений к виду, в котором максимально проявляется внутренний параллелизм. Компилятор старается уменьшить высоту деревьев выражений за счет роста вширь.
Ну и не забудем про традиционные техники оптимизации, которые не ориентированы на регистры и их распределение.
Для того, чтобы разобраться, как это может быть реализовано, взглянем на те
возможности, которые предоставляет нам ассемблер LLVM. Не собираемся же мы в самом деле игнорировать весь накопленный в этой области “культурный слой”.
LLVM
int a(int m, int n)
{
if (m == 0)
return n + 1;
if (n == 0)
return a(m - 1, 1);
return a(m - 1, a(m, n - 1));
}
; Function Attrs: nounwind readnone
define i32 @a(i32 %m, i32 %n) #0 {
%1 = icmp eq i32 %m, 0
br i1 %1, label %tailrecurse._crit_edge, label %.lr.ph
tailrecurse._crit_edge: ; preds = %tailrecurse.backedge, %0
%n.tr.lcssa = phi i32 [ %n, %0 ], [ %n.tr.be, %tailrecurse.backedge ]
%2 = add nsw i32 %n.tr.lcssa, 1
ret i32 %2
.lr.ph: ; preds = %0, %tailrecurse.backedge
%n.tr2 = phi i32 [ %n.tr.be, %tailrecurse.backedge ], [ %n, %0 ]
%m.tr1 = phi i32 [ %4, %tailrecurse.backedge ], [ %m, %0 ]
%3 = icmp eq i32 %n.tr2, 0
%4 = add nsw i32 %m.tr1, -1
br i1 %3, label %tailrecurse.backedge, label %5
; <label>:5 ; preds = %.lr.ph
%6 = add nsw i32 %n.tr2, -1
%7 = tail call i32 @a(i32 %m.tr1, i32 %6)
br label %tailrecurse.backedge
tailrecurse.backedge: ; preds = %5, %.lr.ph
%n.tr.be = phi i32 [ %7, %5 ], [ 1, %.lr.ph ]
%8 = icmp eq i32 %4, 0
br i1 %8, label %tailrecurse._crit_edge, label %.lr.ph
}
Здесь мы видим одни лишь инструкции потока управления, мест, где могла бы проявиться специфика стековой машины нет (если не считать за таковую вычисление +-1).
А как насчет “бабочки” FFT, (это уже скорее из области data flow)?
for (n = 1; n <= LogN; n++)
{
rw = Rcoef[LogN — n];
iw = Icoef[LogN — n];
if (Ft_Flag == FT_INVERSE) iw = -iw;
in = ie >> 1;
ru = 1.0;
iu = 0.0;
for (j = 0; j<in; j++)
{
for (i = j; i<N; i += ie)
{
io = i + in;
rtp = Rdat[i] + Rdat[io];
itp = Idat[i] + Idat[io];
rtq = Rdat[i] — Rdat[io];
itq = Idat[i] — Idat[io];
Rdat[io] = rtq * ru — itq * iu;
Idat[io] = itq * ru + rtq * iu;
Rdat[i] = rtp;
Idat[i] = itp;
}
sr = ru;
ru = ru * rw — iu * iw;
iu = iu * rw + sr * iw;
}
ie >>= 1;
}
…
Тело самого вложенного циклов ассемблере LLVM
( clang -c b.c -O3 --target=xcore -emit-llvm -S -o b_o3.ll ) выглядит так:
%i.020 = phi i32 [ %76, %.lr.ph21 ], [ %j.025, %.preheader19 ]
%57 = add nsw i32 %i.020, %54
%58 = getelementptr inbounds double* %Rdat, i32 %i.020
%59 = load double* %58, align 4, !tbaa !1
%60 = getelementptr inbounds double* %Rdat, i32 %57
%61 = load double* %60, align 4, !tbaa !1
%62 = fadd double %59, %61
%63 = getelementptr inbounds double* %Idat, i32 %i.020
%64 = load double* %63, align 4, !tbaa !1
%65 = getelementptr inbounds double* %Idat, i32 %57
%66 = load double* %65, align 4, !tbaa !1
%67 = fadd double %64, %66
%68 = fsub double %59, %61
%69 = fsub double %64, %66
%70 = fmul double %ru.023, %68
%71 = fmul double %iu.024, %69
%72 = fsub double %70, %71
store double %72, double* %60, align 4, !tbaa !1
%73 = fmul double %ru.023, %69
%74 = fmul double %iu.024, %68
%75 = fadd double %74, %73
store double %75, double* %65, align 4, !tbaa !1
store double %62, double* %58, align 4, !tbaa !1
store double %67, double* %63, align 4, !tbaa !1
%76 = add nsw i32 %i.020, %ie.028
%77 = icmp slt i32 %76, %N
br i1 %77, label %.lr.ph21, label %._crit_edge22
…
В виде графа зависимостей между инструкциями это выглядит так:
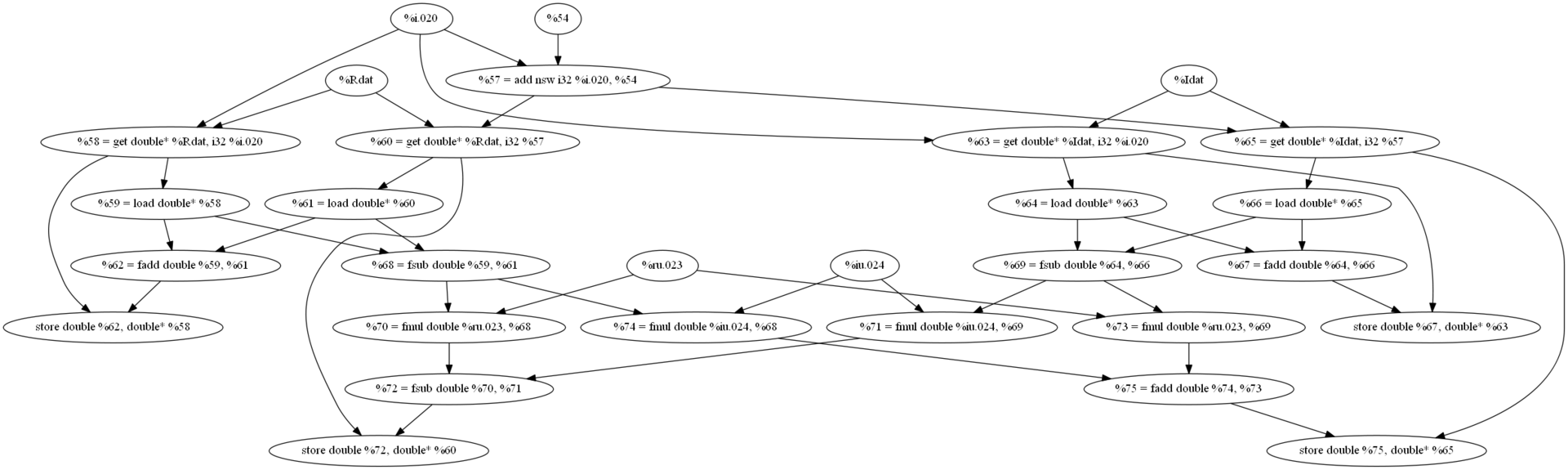
Навскидку, каждая вершина дерева из которой выходит более одного ребра является кандидатом на звание закладки. По крайней мере в том, что касается вычислений с плавающей точкой.
Во всяком случае, реализация описанной архитектуры в LLVM не выглядит безнадёжным мероприятием.
Дот-файл, вдруг пригодится:
L000 [label="%54"];
L001 [label="%Rdat"];
L002 [label="%Idat"];
L003 [label="%ru.023"];
L004 [label="%iu.024"];
L005 [label="%i.020"];
L02 [label="%57 = add nsw i32 %i.020, %54"];
L03 [label="%58 = getelementptr double* %Rdat, i32 %i.020"];
L04 [label="%59 = load double* %58"];
L05 [label="%60 = getelementptr double* %Rdat, i32 %57"];
L06 [label="%61 = load double* %60"];
L07 [label="%62 = fadd double %59, %61"];
L08 [label="%63 = getelementptr double* %Idat, i32 %i.020"];
L09 [label="%64 = load double* %63"];
L10 [label="%65 = getelementptr double* %Idat, i32 %57"];
L11 [label="%66 = load double* %65"];
L12 [label="%67 = fadd double %64, %66"];
L13 [label="%68 = fsub double %59, %61"];
L14 [label="%69 = fsub double %64, %66"];
L15 [label="%70 = fmul double %ru.023, %68"];
L16 [label="%71 = fmul double %iu.024, %69"];
L17 [label="%72 = fsub double %70, %71"];
L18 [label=«store double %72, double* %60»];
L19 [label="%73 = fmul double %ru.023, %69"];
L20 [label="%74 = fmul double %iu.024, %68"];
L21 [label="%75 = fadd double %74, %73"];
L22 [label=«store double %75, double* %65»];
L23 [label=«store double %62, double* %58»];
L24 [label=«store double %67, double* %63»];
L005->L02; L000->L02; L005->L03; L001->L03;
L03->L04; L001->L05; L02->L05; L05->L06; L04->L07;
L06->L07; L002->L08; L005->L08; L08->L09; L002->L10;
L02->L10; L10->L11; L09->L12; L11->L12; L04->L13;
L06->L13; L09->L14; L11->L14; L003->L15; L13->L15;
L004->L16; L14->L16; L15->L17; L16->L17; L17->L18;
L003->L19; L14->L19; L004->L20; L13->L20; L19->L21;
L20->L21; L10->L22; L21->L22; L07->L23; L03->L23;
L08->L24; L12->L24; L05->L18;
}
Эпилог
Вот мы и подошли к предварительному финишу.
Разобрались почему нужно новая архитектура, предложили вариант решения.
Изначально стоял вопрос, а отвечает ли эта архитектура поставленным требованиям.
И теперь можем ответить, да, по крайней мере в той небольшой части С, которую удалось проверить, мы получили
- ожидаемое упрощение аппаратной части
- внешне незаметную масштабируемость по числу регистров
- а также и по числу функциональных устройств
- потенциальное упрощение компиляторов
На первый (дилетантский) взгляд, не видны принципиальные проблемы, препятствующие реализации такой архитектуры в “железе”.
Мы намеренно не рассматривали такие вещи, как:
- вычисления с плавающей точкой, нужен ли для них отдельный стек, ...
- сохранение состояния процессора при переключении контекста
- прерывания
- ...
Всё это вопросы важные, но менее принципиальные.
А на данный момент автор считает свою задачу выполненной.
Автор: zzeng