Статья по результатам работы от классического результата Аксельрода 1984 года до пары фишек, которые я защищал на конкурсах этой зимой.Теория игр иногда дает совершенно предсказуемые ответы, а иногда нетривиальные вопросы, которые, сильно прищурившись, может задать даже школьник, способный дать забавные и довольно доказательные картинки отношений между… да кем угодно! Это и мотивировало меня взять в качестве первой проектной работы математическую игру «Дилемма заключенных».
Читать полностью »
Рубрика «математика» - 199
«Расширенная дилемма заключенных» или «Почему нужно прощать»
2013-04-29 в 12:44, admin, рубрики: математика, теория игр, метки: математика, теория игрРазрезание на две равные части, часть первая
2013-04-29 в 12:34, admin, рубрики: геометрия, комбинаторная геометрия, математика, ололошечки и бугагашечки, метки: геометрия, комбинаторная геометрия, математика, ололошечки и бугагашечкиЗадачи на разрезание — это та область математики, где, как говорится, мамонт не валялся. Множество частных задач, но практически нет общей теории. Помимо всем известной теоремы Бойяи-Гервина, других фундаментальных результатов в этой области практически нет. Неопределённость — вечный спутник задач на разрезание. Мы можем, например, разрезать правильный пятиугольник на шесть частей, из которых можно сложить квадрат; однако мы не можем доказать, что пяти частей для этого было бы недостаточно.
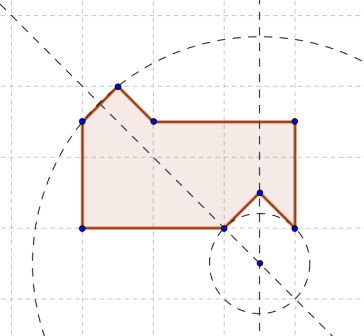
С помощью хитрой эвристики, воображения и поллитры нам порой удаётся найти конкретное решение, но, как правило, мы не обладаем подходящим инструментарием, чтобы доказать минимальность этого решения или же его несуществование (последнее, разумеется, относится к случаю, когда мы решение не нашли). Это печально и несправедливо. И как-то раз я взял чистую тетрадку и решил восстановить справедливость в масштабах одной конкретной задачи: разрезания плоской фигуры на две равных (конгруэнтных) части. В рамках этого цикла статей (их, кстати, будет три) мы с вами, камрады, рассмотрим вот этот забавный многоугольник, изображённый ниже, и попытаемся беспристрастно разобраться, можно ли разрезать его на две равных фигуры, или же таки нет.
OpenFOAM с точки зрения программиста-физика
2013-04-26 в 4:38, admin, рубрики: Блог компании Intel, математика, Программирование, физика, численные методы, метки: математика, физика, численные методы 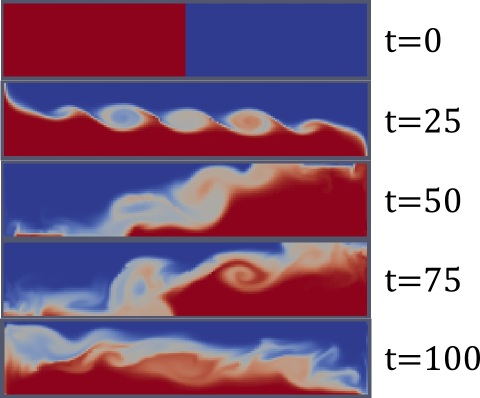
В компании Intel разрабатывается довольно много ПО для моделирования различных физических процессов. В некоторых из них мы используем пакет OpenFOAM, и в этом посте я постараюсь дать краткое описание его возможностей.
Что такое OpenFOAM? Это, пользуясь термином Википедии, открытая (GPL) платформа для численнного моделирования — в первую очередь для моделирования, связанного с решением уравнений в частных производных методом конечных объемов, и в самую первую очередь — для решения задач механики сплошных сред.
КПДВ: эволюция двух несмешивающихся жидкостей разной плотности, изначально разделенных тонкой перегородкой (пример «lockExchange» из стандартной поставки OpenFOAM). Переходные цвета обозначают ячейки сетки, где присутствует доля и той, и другой жидкости (более точно: при симуляции используется метод объёма жидкости).
Стивен Вольфрам провёл математический анализ социальных сетей
2013-04-25 в 7:43, admin, рубрики: data mining, Facebook, жизнь, математика, Социальные сети и сообщества, социальный граф, метки: жизнь, математика, социальный граф 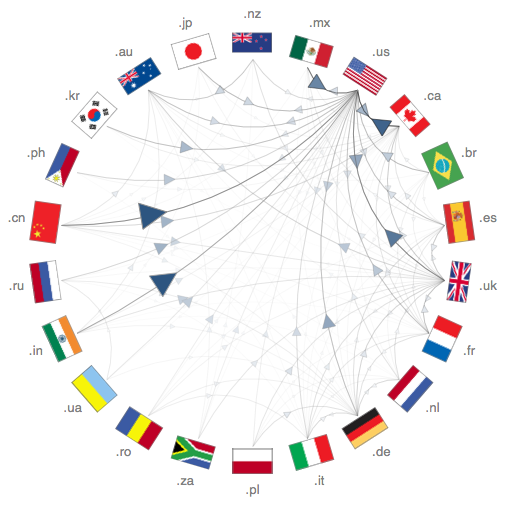
Изменение места жительства пользователей Facebook
Математик и программист Стивен Вольфрам известен как автор программы Mathematica и научного поисковика Wolfram Alpha. Несмотря на большой объём текущей работы, Стивена всегда интересовал вопрос: можно ли математическими методами проанализировать траекторию жизни человека. В прошлом году он сделал первую попытку и опубликовал результаты анализа своих личных цифровых данных: визуализация 300 тыс. отправленных электронных писем с 1989 года, 100 миллионов нажатий клавиш с 2002 года, телефонные звонки, встречи, время редактирования файлов разного типа с 1980 года и т.д. Подобный личностный анализ доступен для всех подписчиков на платную версию Wolfram Alpha Pro.
Теперь пришло время перейти расширить концепцию личностного анализа на обработку данных с социальных сетей. Недавно на поисковике Wolfram Alpha был открыт раздел Personal Analytics for Facebook (персональная аналитика для Facebook), а в программный пакет Mathematica добавили функцию SocialMediaData. Уже есть первые результаты.
Читать полностью »
Вероятностные модели: примеры и картинки
2013-04-25 в 6:26, admin, рубрики: data mining, байесовские сети, Блог компании Surfingbird, искусственный интеллект, математика, математическое моделирование, теория вероятностей, метки: data mining, байесовские сети, математика, математическое моделирование, теория вероятностейСегодня – вторая серия цикла, начатого в прошлый раз; тогда мы поговорили о направленных графических вероятностных моделях, нарисовали главные картинки этой науки и обсудили, каким зависимостям и независимостям они соответствуют. Сегодня – ряд иллюстраций к материалу прошлого раза; мы обсудим несколько важных и интересных моделей, нарисуем соответствующие им картинки и увидим, каким факторизациям совместного распределения всех переменных они соответствуют.
Порождающие грамматики Хомского
2013-04-24 в 18:05, admin, рубрики: Алгоритмы, математика, ПрограммированиеНебольшое предисловие
Этот текст является продолжением поста , в котором автор попытался как можно более просто и без сложных математических выкладок описать понятия формального языка и грамматики. На этот текст пришло достаточно много откликов и автор счел себя обязанным написать продолжение.
Ниже описывается формализм порождающих грамматик Хомского. Методы задания языка с помощью порождающих грамматик сейчас довольно популярны, особенно для машинной обработки компьютерных языков. Но обычно изучение порождающих грамматик в теории трансляторов заканчивается на контекстно-свободных грамматиках. Последние являются довольно узким специальным классом порождающих грамматик Хомского и обычно используются как вид категориальных грамматик (как конкретно это делается, будет показано ниже) для задания синтаксических анализаторов. Последнее обстоятельство только затуманивает понимание подхода Хомского. Дальнейшее изложение предназначено тем, кому интересно понять, в чем состоит этот подход.
Готовы ли мы все перейти на электрокары (задача Ферми)
2013-04-23 в 8:35, admin, рубрики: математика, экология, Энергия и элементы питания, метки: экологияЯ сам пытаюсь быть где-то посредине между «глобальными заговорщиками» и нашими «борцами за экологию», ибо считаю, что истина где-то именно там…
Недавно был День Земли и, почитав немного на Википедии о Часе Земли и, особенно, раздел Критика, я дошел до интересной статьи Константина Ранкса Как вредит экологии борьба с глобальным потеплением. Там утверждается, что современная мощность автомобилей в 37 раз больше мощности все электростанций мира. Откуда взяты данные для этих расчетов — не сказано. Захотелость проверить самому, но как? Гуглить в поисках исходных данных? Можно, но долго, ненадежно и скучно. Есть и другой путь, не менее интересный!
Как-то еще в школе в «Кванте» читал статейку о задачах Ферми и ее классический пример о количестве молекул резины, стираемых за один оборот колеса. Вот и захотелось попробовать применить этот же метод и «прикинуть» числа в нашем случае.
Скорее всего, я не учел много фактов, о которых вы позже укажете в комментариях, но, как я и писал выше, истину найдем где-то посредине…
Читать полностью »
Классификация методов и моделей прогнозирования
2013-04-23 в 7:08, admin, рубрики: математика, прогнозирование временных рядов, метки: прогнозирование временных рядовЯ занимаюсь прогнозированием временных рядов уже более 5 лет. В прошлом году мною была защищена диссертация по теме «Модель прогнозирования временных рядов по выборке максимального подобия», однако вопросов после защиты осталось порядочно. Вот один из них — общая классификация методов и моделей прогнозирования.
Обычно в работах как отечественных, так и англоязычных авторы не задаются вопросом классификации методов и моделей прогнозирования, а просто их перечисляют. Но мне кажется, что на сегодняшний день данная область так разрослась и расширилась, что пусть самая общая, но классификация необходима. Ниже представлен мой собственный вариант общей классификации.
В чем разница между методом и моделью прогнозирования?
Метод прогнозирования представляет собой последовательность действий, которые нужно совершить для получения модели прогнозирования. По аналогии с кулинарией метод есть последовательность действий, согласно которой готовится блюдо — то есть сделается прогноз.
Модель прогнозирования есть функциональное представление, адекватно описывающее исследуемый процесс и являющееся основой для получения его будущих значений. В той же кулинарной аналогии модель есть список ингредиентов и их соотношение, необходимый для нашего блюда — прогноза.
Совокупность метода и модели образуют полный рецепт!
В настоящее время принято использовать английские аббревиатуры названий как моделей, так и методов. Например, существует знаменитая модель прогнозирования авторегрессия проинтегрированного скользящего среднего с учетом внешнего фактора (auto regression integrated moving average extended, ARIMAX). Эту модель и соответствующий ей метод обычно называют ARIMAX, а иногда моделью (методом) Бокса-Дженкинса по имени авторов.
Сначала классифицируем методы
Если посмотреть внимательно, то быстро выясняется, что понятие «метод прогнозирования» гораздо шире понятия «модель прогнозирования». В связи с этим на первом этапе классификации обычно делят методы на две группы: интуитивные и формализованные [1].
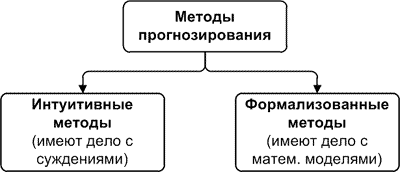
Если мы вспомним нашу кулинарную аналогию, то и там можно разделить все рецепты на формализованные, то есть записанные по количеству ингредиентов и способу приготовления, и интуитивные, то есть нигде не записанные и получаемые из опыта кулинара. Когда мы не пользуемся рецептом? Когда блюдо очень просто: пожарить картошку или сварить пельмени — тут рецепт не нужен. Когда еще мы не пользуемся рецептом? Когда желаем изобрести что-то новенькое!
Интуитивные методы прогнозирования имеют дело с суждениями и оценками экспертов. На сегодняшний день они часто применяются в маркетинге, экономике, политике, так как система, поведение которой необходимо спрогнозировать, или очень сложна и не поддается математическому описанию, или очень проста и в таком описании не нуждается. Подробности о такого рода методах можно глянуть в [2].
Формализованные методы — описанные в литературе методы прогнозирования, в результате которых строят модели прогнозирования, то есть определяют такую математическую зависимость, которая позволяет вычислить будущее значение процесса, то есть сделать прогноз.
На этом общая классификация методов прогнозирования на мой взгляд может быть закончена.
Статистические тесты в R. Часть 3: Тесты количественных данных
2013-04-20 в 9:24, admin, рубрики: анализ данных, математика, статистика, Статистика в IT, статистический анализ, метки: анализ данных, математика, статистика, статистический анализЭто третья статья в серии о применении R для статистического анализа данных, в которой будут разбираться представление и тестирование количественных данных. Вы узнаете как быстро и наглядно представить данные, а также как использовать t-тест в R.
Часть 1: Бинарная классифиация
Часть 2: Анализ качественных данных
Поехали!
Читать полностью »
Многочлены от нескольких переменных и алгоритм Бухбергера на Haskell
2013-04-18 в 18:10, admin, рубрики: haskell, алгебра, Алгоритмы, математика, функциональное программирование, метки: haskell, алгебра, функциональное программированиеВ этой статье я хочу рассказать о том, как реализовывал алгоритмы, связанные с базисами Грёбнера, на языке Haskell. Надеюсь кому-нибудь мои идеи и объяснения окажутся полезными. Я не собираюсь вдаваться в теорию, так что читателю стоит быть знакомым с понятиями полиномиального кольца, идеала кольца и базиса идеала. Советую прочитать вот эту книгу МЦНМО, в ней подробно расписана вся необходимая теория.
Основной предмет статьи — базисы Грёбнера идеалов колец многочленов от нескольких переменных. Это понятие возникает при изучении систем полиномиальных уравнений и даёт очень хороший способ для их решения в большинстве случаев. В конце статьи я на примере покажу, как можно применять эти идеи.
Самый главный результат, который даёт эта теория — хороший способ решать полиномиальные системы уравнений от нескольких переменных. Даже если вы не знакомы с высшей алгеброй или с Haskell, я советую вам прочитать эту статью, так как эти самые методы решения объяснены на уровне, доступном школьнику, а вся теория нужна только для обоснования. Можно спокойно пропустить всё, что связано с высшей алгеброй, и просто научиться решать системы уравнений.
Если вас заинтересовало, прошу под кат. Читать полностью »

