Одна из страниц его биографии известна чуть менее широко. Связана она с решением поистине чудовищно сложного для тех времен алгебраического уравнения 45-ой степени!
В 1594 году Виет прославился как математик на всю Европу. Известный голландский математик того времени Адриан ван Роумен предложил математикам Европы решить составленное им уравнение 45-й степени и разослал письменный вызов в разные страны. Во Францию он письмо не отправил, так как считал, что там нет математика, способного решить поставленную задачу.
Само уравнение имело вид:

В современной записи оно выглядит следующим образом:
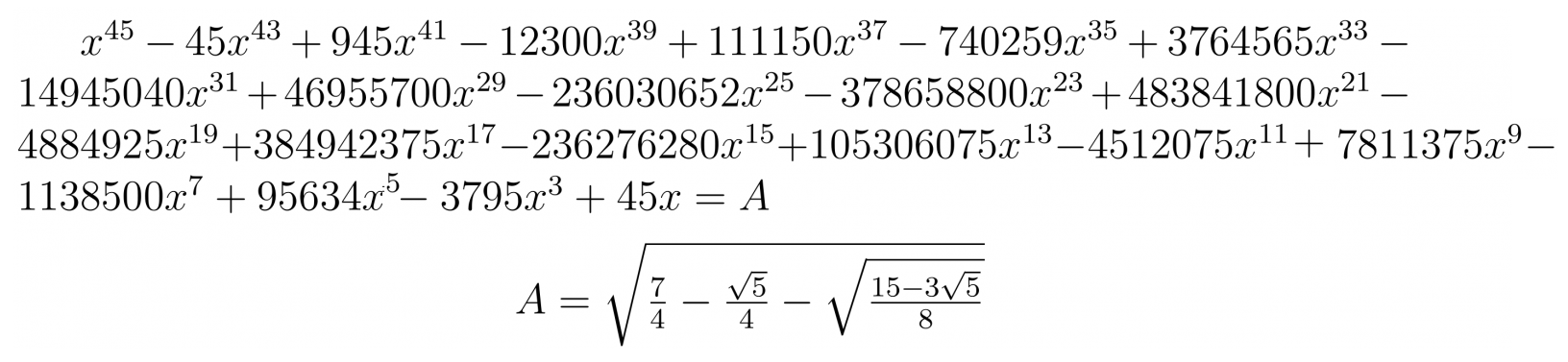
Каждый из коэффициентов велик, и ни один из них не является простым. Девятнадцать из них, например, делятся на 5. 95 634 делится на 7. 236 030 652 делится на 12. 740 259 делится на 3. Кроме того, коэффициенты постепенно увеличиваются к середине. Эту закономерность демонстрируют такие биномы, как (x + y)^n.
Большинство источников не уточняют, каким именно образом ван Роумен придумал это уравнение, ведь, согласитесь, из головы такое взять невозможно. Ответ на этот вопрос мы узнаем, когда прочитаем, чем был известен голландец.

Ван Роумен был профессором математики и медицины с 1586 по 1592 год, а затем в течение шести месяцев в 1592 году был ректором Лёвенского католического университета. За это время он спланировал опубликовать обзор всей математики:
В качестве первой части этого проекта он работал над «theoria polygonorum», теорией правильных многоугольников. Результатом этого должны были стать таблицы синусов, касательных и секущих, а также решение задачи о возведении окружности в квадрат, что для него означало вычисление пропорции между длиной окружности и диаметром окружности. Предполагалось, что работа будет состоять из 12 глав, в первых четырех из которых будут рассмотрены правильные 3-, 4-, 5- и 15-угольники и связанные с ними многоугольники, полученные многократным удвоением числа сторон. В разделах 5-9 рассматриваются все остальные правильные многоугольники. В главах 10 и 11 ван Румен изучал круг. В 10 разделе будет рассказано, как вычислить его окружность и площадь. В 11 разделе будут рассмотрены многие ошибочные или просто неправильные решения проблемы возведения круга в квадрат. Наконец, в разделе 12 будет показано, как необходимые арифметические операции могут быть выполнены с наименьшими трудностями.
Оказывается, традицией того времени было завуалированно сообщать о своих открытиях. Именно эту цель и преследовал ван Роумен. Получив новую общую формулу для составления таблиц тригонометрических функций, он просто свёл к уравнению одно из вычисленных им значений.
В защиту этой позиции есть неопровержимый факт. Ван Роумен привёл в письме несколько решений уравнения при других значениях правой части, например:
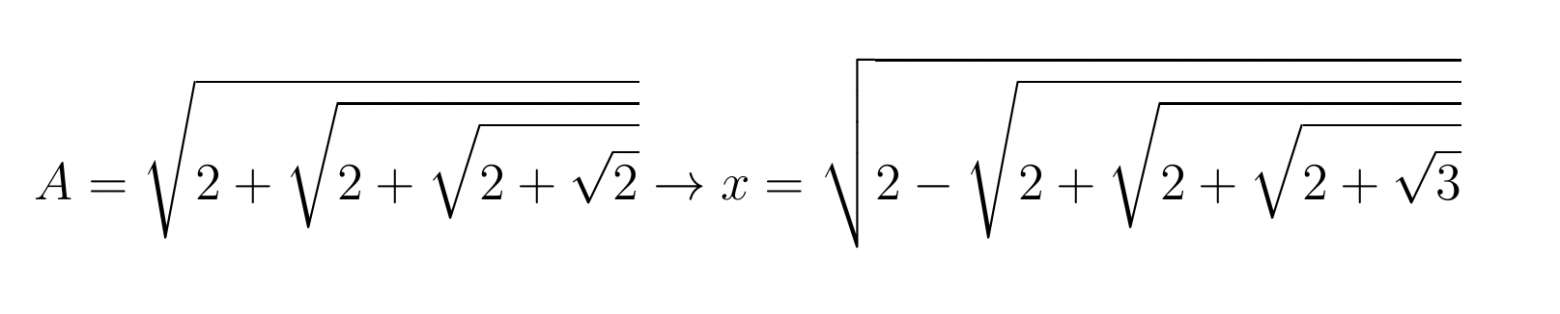
Уравнение ван Роумена было упомянуто на встрече голландского посла с королем Франции Генрихом IV. Посол Нидерландов тогда отметил, что «ни один французский математик не был включен в составленный ван Роуменом обзор великих математиков». Возмущенный монарх ответил, «что их есть у нас» и поручил передать задачу Виету. Посмотрим же, как Франсуа мог расколоть этот «крепкий орешек».
❯ Левая часть уравнения
Гениальность француза, решившего это уравнение практически сразу, заключалась в том, что он вывел формулу, по которой в левой части получаются коэффициенты при х. Используя современные обозначения:

Некоторые источники говорят, что этот алгебраический вывод — следствие величайшей геометрической интуиции Виета, связавшего уравнение с построением правильных вписанных многоугольников.
Оценив количество множителей в левой части уравнении Виет определил, что n=45… Если хочется убедиться в справедливости формулы, то пожалуйста:
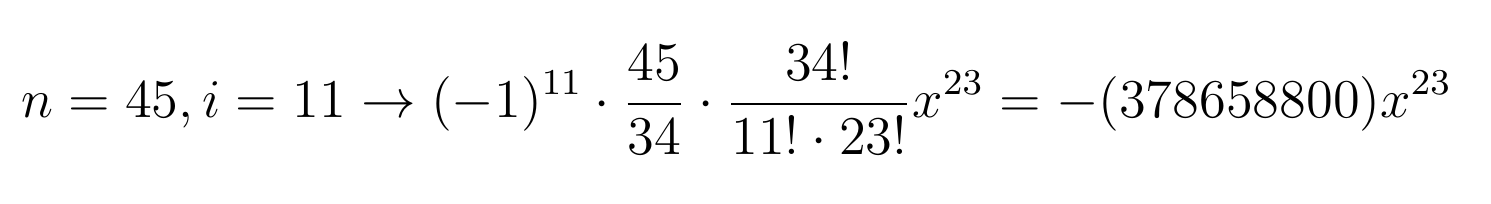
Все остальные коэффициенты получаются аналогичным образом.
❯ Правая часть уравнения
Зацепившись за примеры решения уравнения, которые были представлены ван Роуменом в письме, Виет «почуял» тригонометрию. Выкладки были примерно такие:
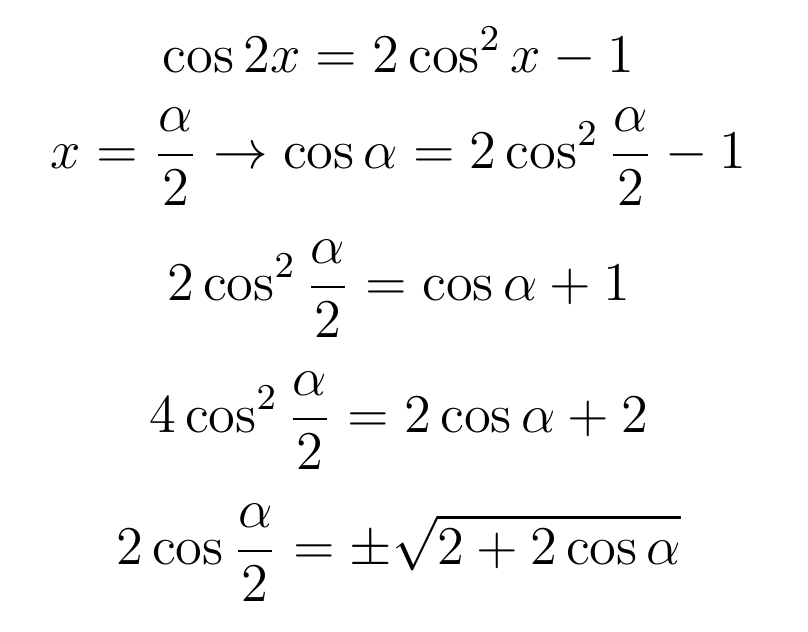
Врубив рекурсию на максимум, Виет смог показать, что значение А, которое было приведено выше, не что иное, как:
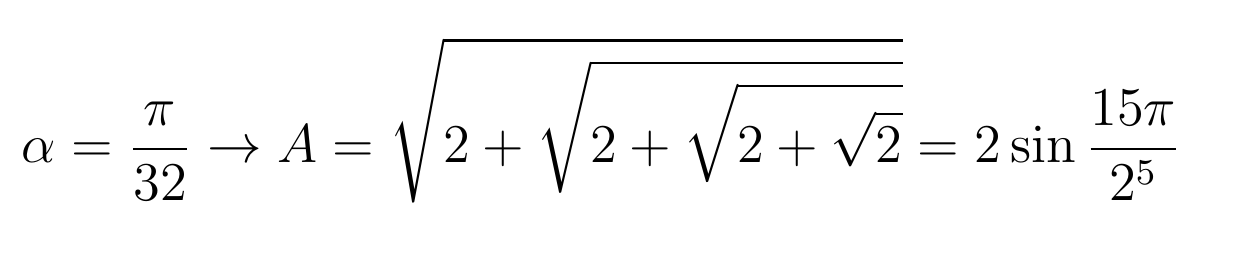
Оставив любопытному читателю все остальные преобразования, покажу, чего добился Виет со значением А из исходного уравнения:
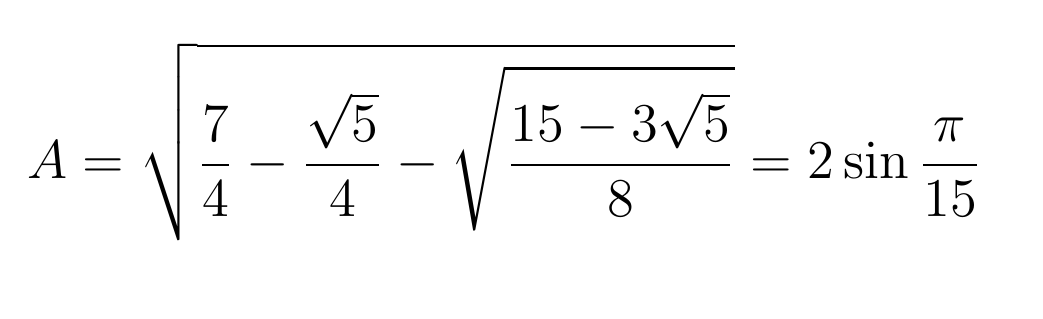
Теперь вернемся к общей формуле, вычисляющей коэффициенты разложения. В первом множителе там число 45, втрое большее знаменателя выше, что наводит на общую формулу:
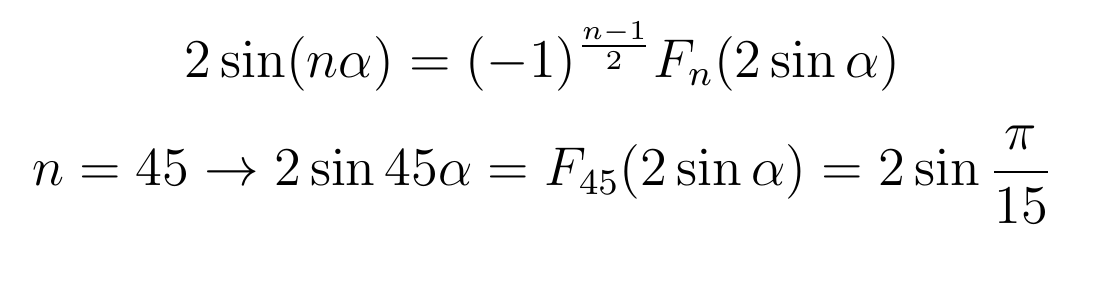
Вместо х, как в исходном уравнении, подставлен удвоенный синус. Приравнивая, получим:
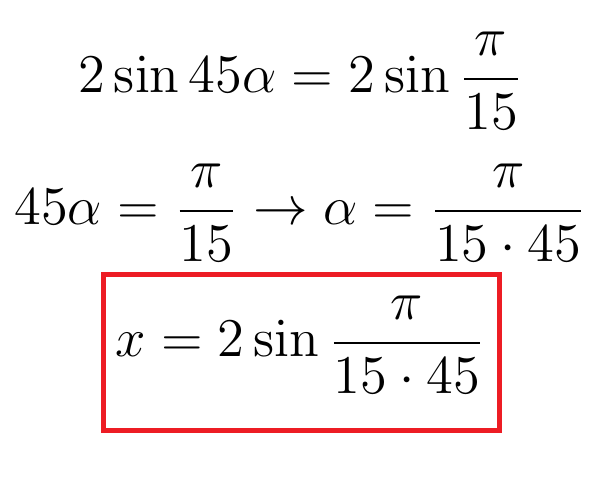
Но синус — функция периодическая, и у этого уравнения Виет нашел еще 44 решения, все из них вида:
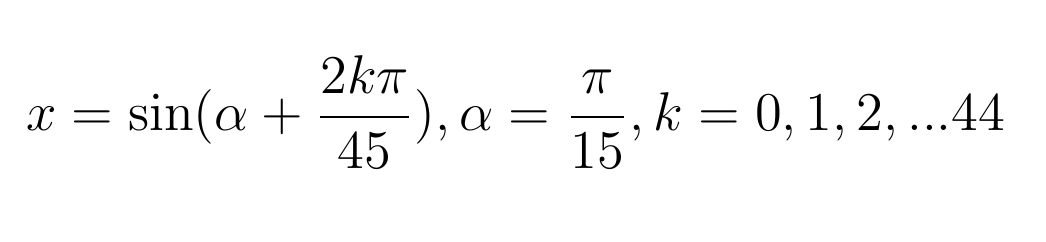
Франсуа, впрочем, признал только 22 положительных решениях, потому что отрицательные вовсе не считал нужным показывать. Если учесть, что алгебраическая символика еще была несовершенной, не было обозначений тригонометрических функций, не было удобного обозначения радикалов, то решение Виетом уравнения ван Роумена действительно вызывает восхищение. Как результат, Виет прославился на всю Европу и значительно повысил авторитет французских математиков.
- Больше математики в Telegram — "Математика не для всех".
Автор:
andreybrylb