Введение
Имитационное обучение с использованием мультимедийных образовательных ресурсов является одним из перспективных направлений информатизации современного образования. Под имитационным обучением мы будем понимать такую модель обучения, в которой посредством программного обеспечения виртуально воспроизводятся физические процессы и условия, аналогичные реальным, но имеющие ряд идеализированных качеств. Возможность интерактивного взаимодействия с виртуальной моделью того или иного физического процесса позволяет существенно понизить уровень абстракции знаний о данном процессе, в результате чего повышается эффективность получения и усвоения этих знаний человеком [1].
Объект изучения и постановка задачи
В качестве объекта изучения рассмотрим один из наиболее важных разделов общей физики – классическую термодинамику. В контексте образовательной деятельности знания по данной дисциплине преподаются в нескольких формах, основными из которых являются: консолидированный теоретический материал в виде лекций и учебных пособий; практические задания в виде сборников задач и тестов; лабораторный практикум в виде методических указаний к выполнению лабораторных экспериментов по темам основной теории. Перечисленные формы преподавания отличаются уровнем абстракции передаваемой информации, и в своей совокупности формируют наиболее полную картину знаний по изучаемой дисциплине.
Наиболее требовательной в плане методологии и технической реализации формой знаний является лабораторный практикум. С этой целью при университетах и колледжах создаются специально оборудованные учебные лаборатории, полностью отвечающие требованиям образовательного процесса. Своевременный доступ к данным лабораториям, как правило, осуществляется в процессе прохождения студентами обучения в очной форме. Возможность работы в учебных лабораториях неотъемлемо связана с необходимостью физического присутствия обучаемого в помещении лаборатории, а также высокой стоимостью содержания и обслуживания лаборатории в условиях её интенсивной эксплуатации.
При прохождении студентом дистанционного обучения, или автономного обучения без помощи образовательной организации, возможность выполнения лабораторных экспериментов зачастую полностью отсутствует. Как показывает практика, в данном случае обучаемый знакомится с лабораторными экспериментами посредством видеозаписей или анимаций, найденных (по возможности) в свободном доступе сети Интернет, что является малоэффективным способом изучения требуемого учебного материала ввиду отсутствия интерактивности и структурированности материала, а зачастую, языковых ограничений и низкого качества изложенного материала.
В силу вышеизложенного, актуальной задачей для разработчиков мультимедийных образовательных ресурсов становится создание такого средства обучения, которое обеспечивало бы образовательный процесс всеми необходимыми функциями в части выполнения экспериментальной работы, содержало в себе структурированный методический материал, способствовало эффективному усвоению знаний в той или иной изучаемой области. С технической стороны данное средство обучения должно обладать гибкостью интеграции в различные системы дистанционного обучения (в форме веб-приложений и программных компонентов), возможностью выполнения на мобильных устройствах и персональных компьютерах, высокой производительностью и простотой управления.
Пример реализации имитационной модели лабораторного эксперимента
Рассмотрим лабораторный эксперимент «Реальные газы и точка фазового перехода» из курса термодинамики для студентов и учеников старших классов общеобразовательных школ. Целью данного эксперимента является количественный анализ реального газа (шестифтористой серы SF6) и определение его точки фазового перехода. Лабораторный опыт выполняется на лабораторной установке (рисунок 1) производства компании 3B Scientific [2].

Рисунок 1 – Внешний вид реального аналога лабораторной установки по определению точки фазового перехода реального газа
Представленная лабораторная установка оснащена газовым резервуаром, стрелочным манометром для измерения давления газа в резервуаре, подвижным поршнем с винтовым механизмом и шкалой, системой клапанов и электронным термометром для измерения температуры газа. Вращением маховика осуществляется перемещение поршня, что в свою очередь изменяет свободный объем газового резервуара. Рабочая часть газового резервуара выполнена из полупрозрачного материала, что позволяет визуально наблюдать состояние исследуемого вещества в процессе эксперимента.
Точка фазового перехода реального газа характеризуется критической температурой, критическим давлением и критической плотностью. Ниже критической температуры вещество находится в газообразном состоянии при больших объемах и в жидком состоянии при маленьких объемах. При промежуточных объемах оно может существовать как смесь жидкости и газа, в которой изменение объема в изотермических условиях вызывает изменение агрегатного состояния: газообразная фракция увеличивается с увеличением объема, а давление смеси остается постоянным. Поскольку жидкость и пары имеют разные плотности, они разделяются в поле тяготения. По мере повышения температуры плотность жидкости уменьшается, а плотность газа возрастает, пока эти две плотности не станут равными одному и тому же значению критической плотности. Выше критической температуры газ невозможно перевести в жидкое состояние. Однако в изотермических условиях газ не подчиняется законам идеального газа, пока его температура не поднялась значительно выше критической температуры.
Состояние газа в зависимости от параметров давления (P), объема (V) и температуры (T) представляется с помощью фазовой диаграммы Клайперона. В качестве математической основы эксперимента используется модель газа Ван-дер-Ваальса:
$$display$$Pr(Vr)=8Tr/(3Vr-1)-3/Vr^2$$display$$
где Pr – приведенное давление газа, равное отношению его фактического давления к давлению в критической точке (Pr=P/Pc); Vr – приведенный объем газа, равный отношению его фактического объема к объему в критической точке (Vr=V/Vc); Tr – приведенная температура газа, равная отношению его фактической температуры к температуре в критической точке (Tr=T/Tc).
Уравнение Ван-дер-Ваальса позволяет рассчитать изотермы (линии равной температуры) для исследуемого газа в приведенной форме (рисунок 2).
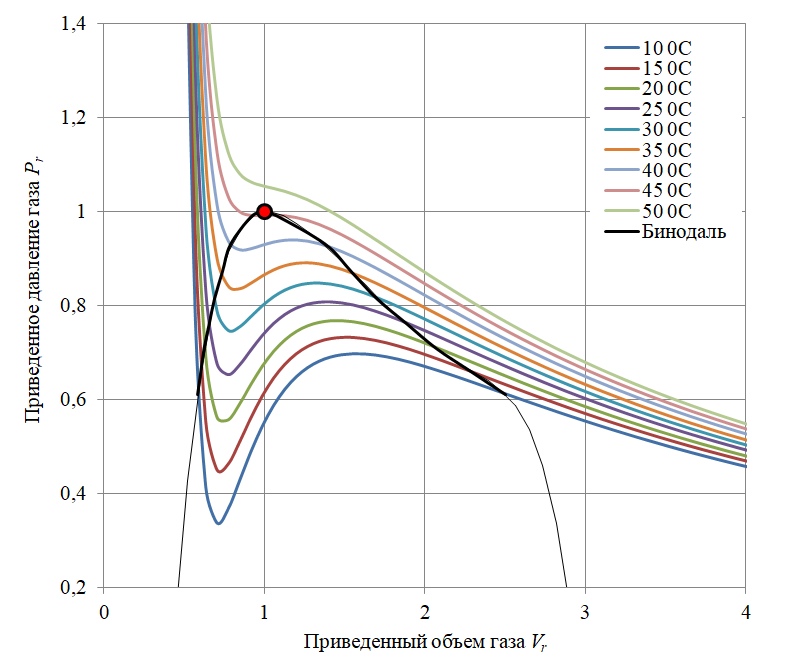
Рисунок 2 – Фазовая диаграмма Клайперона для шестифтористой серы SF6 без учета парожидкостного равновесия
Как видно из диаграммы на рисунке 2, при температуре газа ниже критической (Tc), уравнение Ван-дер-Ваальса в той части изотермы, где dPr/dVr>0, имеет колебательный характер. На данных участках вещество находится в форме смеси газа и жидкости, и в реальности конденсация газа происходит по изобарическому пути (объем изменяется при постоянном давлении). Таким образом, диаграмма Ван-дер-Ваальса в пределах так называемой бинодальной кривой (черная кривая на диаграмме) [3] неадекватно описывает поведение реального газа.
Для решения данной задачи использовался метод равных площадей Максвелла [4], суть которого заключается в замещении колеблющегося участка изотермы горизонтальной линией (изобарой), разделяющей площадь, описанную изотермой, на две площади равной величины (рисунок 3).
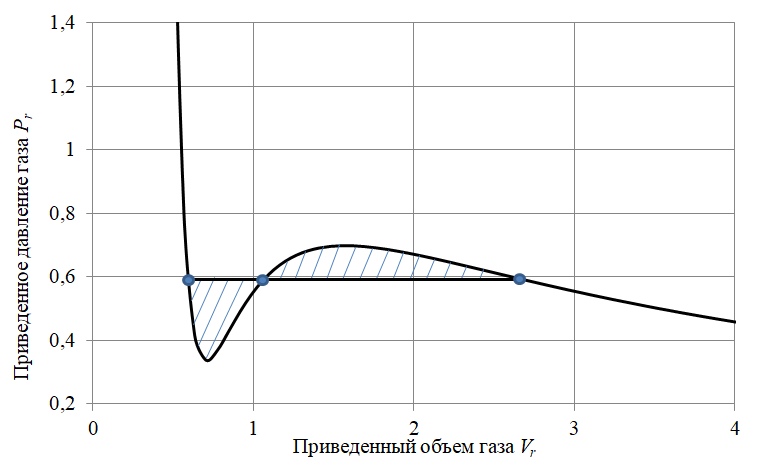
Рисунок 3 – К методу равных площадей Максвелла
Ниже представлен фрагмент программного кода (Matlab) для решения описанной задачи [4].
function maxwell_equal_area_2
clc; clear all; close all
% температура Tr ниже Tc: Tr = T/Tc
Tr = 0.9;
% аналитическое выражение для Pr (упрощенное уравнение Ван-дер-Ваальса)
Prfh = @(Vr) 8/3*Tr./(Vr - 1/3) - 3./(Vr.^2);
% вектор изменения объема
Vr = linspace(0.5,4,100);
% вектор изменения давления
Pr = Prfh(Vr);
Для вычисления площадей двух областей, образованных изотермой и изобарой, необходимо найти три корня полиномиального уравнения:
$$display$$Vr^3-(1+8Tr/Pr)/3+3/Pr-1/Pr=0$$display$$
% вектор коэффициентов уравнения
vdWp = [1 -1/3*(1+8*Tr/y) 3/y -1/y];
% сортировка корней по возрастанию
v = sort(roots(vdWp))
% площадь A1 (площадь под изобарой за вычетом площади под изотермой)
A1 = (v(2)-v(1))*y - quad(Prfh,v(1),v(2))
% площадь A2 (площадь под изотермой за вычетом площади под изобарой)
A2 = quad(Prfh,v(2),v(3)) - (v(3)-v(2))*y
% функция, равная нулю, при условии, что A1=A2
Pr_equal_area = fzero(@equalArea, 0.65)
Результаты вычислений можно отобразить на диаграмме (рисунок 4).
xx = [v(1) Vr(Vr >= v(1) & Vr <= v(2)) v(2)];
yy = [Prfh(v(1)) Pr(Vr >= v(1) & Vr <= v(2)) Prfh(v(2))];
lightgray = [0.9 0.9 0.9];
fill(xx,yy,lightgray)
xx = [v(2) Vr(Vr >= v(2) & Vr <= v(3)) v(3)];
yy = [Prfh(v(2)) Pr(Vr >= v(2) & Vr <= v(3)) Prfh(v(3))];
fill(xx,yy,lightgray)
% текстовые метки для обозначения площадей
text(v(1),1,sprintf('A1 = %f',A1))
text(v(3),1,sprintf('A2 = %f',A2))
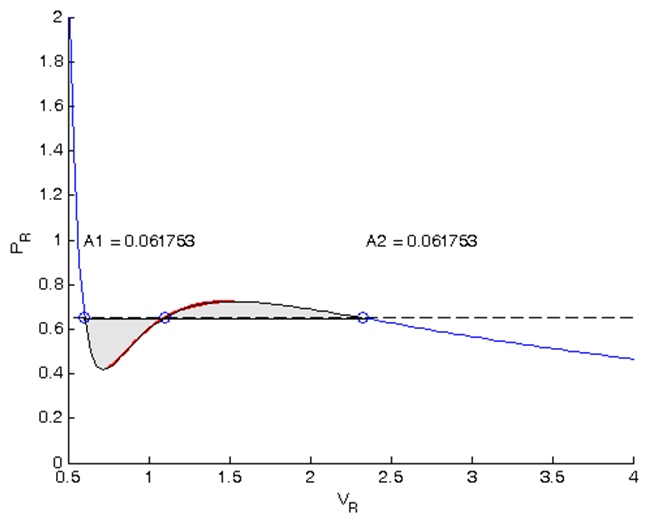
Рисунок 4 – Результаты расчета изобары по методу равных площадей Максвелла в среде Matlab
Окончательный вид функции для метода равных площадей:
function Z = equalArea(y)
Tr = 0.9;
vdWp = [1 -1/3*(1+8*Tr/y) 3/y -1/y];
v = sort(roots(vdWp));
Prfh = @(Vr) 8/3*Tr./(Vr - 1/3) - 3./(Vr.^2);
A1 = (v(2)-v(1))*y - quad(Prfh,v(1),v(2));
A2 = quad(Prfh,v(2),v(3)) - (v(3)-v(2))*y;
Z = A1 - A2;
% категория: нелинейная алгебра; тэг: термодинамика
Таким образом, окончательная математическая модель эксперимента представляется диаграммой Клайперона для шестифтористой серы с учетом условия парожидкостного равновесия (рисунок 5).
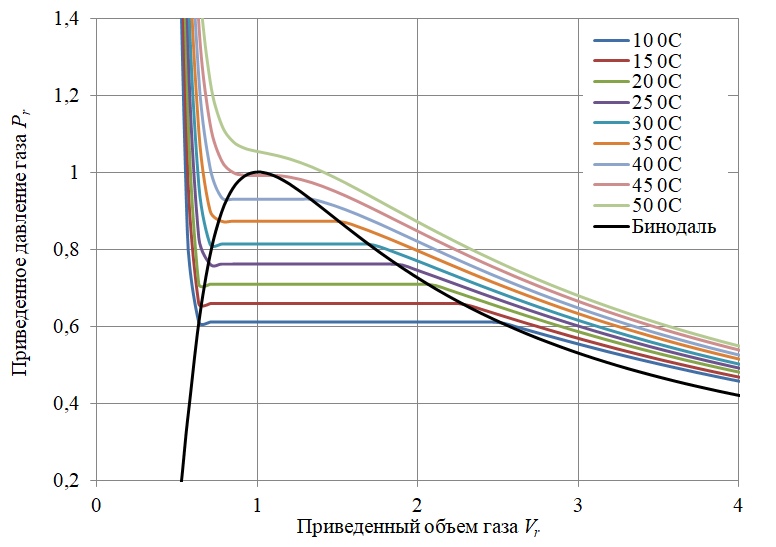
Рисунок 5 – Фазовая диаграмма Клайперона для шестифтористой серы SF6 с учетом парожидкостного равновесия
Наряду с математической составляющей, имитационная модель эксперимента включает комплекс графических объектов, визуально отражающих лабораторное оборудование (рисунок 6).

Рисунок 6 – Графическая модель лабораторной установки: 1 – манометр; 2 – циркуляционный термостат; 3 – электронный термометр; 4 – газовый резервуар; 5 – механизм регулирования объема; 6 – клапан заправки газа
К измеряемым величинам в режиме выполнения эксперимента добавляются динамически генерируемые погрешности, имитирующие переходные (нестационарные) процессы, неточности измерений, чувствительность органов управления и т.д. Имитационная модель полностью обеспечивает наблюдение физического процесса с возможностью изменения входных параметров и условий эксперимента.
Пример реализации виртуального лабораторного практикума
На основе описанного выше примера методологии расчета имитационных моделей физических процессов, с использованием языка программирования высокого уровня AppGameKit разработан интерактивный лабораторный практикум классической термодинамики, охватывающий основные темы курса: внутренняя энергия, законы газов, перенос тепла, тепловое расширение, термодинамические циклы. Данная разработка предназначена для проведения лабораторных экспериментов в условиях отсутствия реального лабораторного оборудования. Лабораторные установки выполнены в соответствии с их реальными аналогами. Каждая лабораторная работа включает краткие методические указания и справочные сведения, необходимые для обработки экспериментальных данных.
Отличительной особенностью виртуальной лаборатории является её имплементарная гибкость, обусловленная мультиплатформенной поддержкой. Выполнение имитационных лабораторных работ возможно на персональных компьютерах, мобильных устройствах и в среде веб-браузера (без необходимости установки программного обеспечения на устройство пользователя). В представленном решении используется уникальный алгоритм загрузки в память графической 3D сцены с использованием собственного формата данных в бинарном виде, позволяющий сократить время реконструкции 3D моделей в игровом движке до нескольких секунд, что является немаловажным фактором при выполнении программы на мобильных устройствах.
На рисунке 7 представлен фрагмент экрана, демонстрирующий выполнение виртуальной лаборатории в веб-браузере Microsoft Edge, обеспечивающим полноценную аппаратную поддержку 3D графики на основе стандарта HTML5 и технологии WebGL.
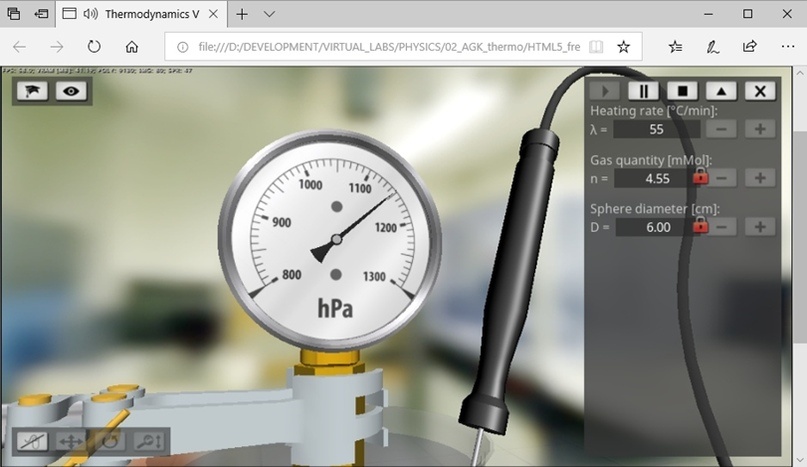
Рисунок 7 – Выполнение виртуальной лаборатории в веб-браузере Microsoft Edge
Ниже представлены онлайн-версии лабораторных работ, для выполнения которых рекомендуется использовать веб-браузер Microsoft Edge, входящий в состав операционной системы Microsoft Windows 10:
- Внутренняя энергия и механическая работа
- Внутренняя энергия и работа электрического тока
- Закон Бойля-Мариотта
- Закон Гей-Люссака
- Показатель адиабаты воздуха
- Реальные газы и точка фазового перехода
- Куб Лесли
- Теплопроводность
- Тепловое расширение твердых тел
- Аномалия воды
- Двигатель Стирлинга модели D
- Двигатель Стирлинга модели G
- Тепловые насосы
Для выполнения лабораторных работ на мобильном устройстве (смартфоне или планшете) на базе операционной системы Android можно загрузить мобильное приложение виртуальной лаборатории.
Заключение
Описанный в данной статье пример реализации средства имитационного обучения на основе виртуальной лаборатории термодинамики демонстрирует возможность дополнения образовательного процесса вспомогательным методологическим инструментом, отвечающим требованиям и стандартам современного общего и высшего образования. Обобщенная концепция разработки мультимедийных образовательных ресурсов включает ряд основных этапов: определение актуальной методологической составляющей лабораторного практикума (в том числе выбор эффективного лабораторного оборудования и его справочно-методического сопровождения); разработка имитационно-численной модели эксперимента; реализация графической составляющей имитационного лабораторного практикума; реализация программной составляющей имитационного лабораторного практикума; интеграция имитационного лабораторного практикума в образовательный процесс (внедрение разработки в существующий учебный курс или создание нового учебного курса, ориентированного на работу с имитационным лабораторным практикумом).
Одним из перспективных направлений развития технологии имитационного обучения на данный момент являются реализация мультиагентных обучающих систем, работа которых основана алгоритмах генерации индивидуальных образовательных траекторий с динамическим формированием учебного контента. Такие системы предусматривают адаптивную настройку среды обучения, учитывающую индивидуальные особенности профиля пользователя. Данные алгоритмы позволят получить: для студентов – персонифицированные план, контент, методику и инструменты электронного обучения; для преподавателей – инновационные технологии преподавания и анализа формируемых компетенций, для школ и университетов – современную модель управления образовательным процессом.
Библиографические ссылки
- Виртуальные лаборатории и технические симуляторы
- Лабораторное оборудование 3B Scientific
- Метод расчета бинодальных кривых
- Метод равных площадей для уравнения Ван-дер-Ваальса
Автор: SunSpire






