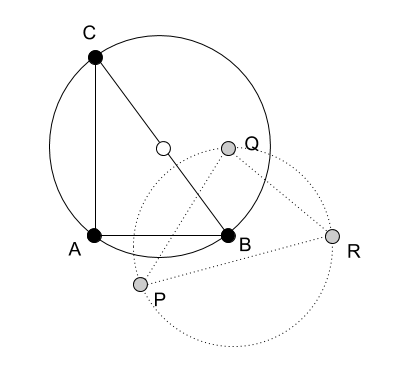
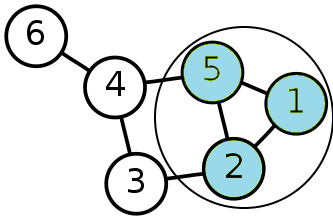
Как построить топологию сети на канальном уровне, если в нужной подсети используются только неуправляемые свитчи? В статье я постараюсь ответить на этот вопрос.
Начну с причины возникновения LLTR (Link Layer Topology Reveal).
У меня был один “велосипед” - синхронизатор больших файлов “на полной скорости сети”, способный за 3 часа целиком залить 120 GiB файл по Fast Ethernet (100 Мбит/с; 100BASE‑TX; дуплекс) на 1, 10, 30, или 200 ПК. Это был очень полезный “велосипед”, т.к. скорость синхронизации файла почти не зависела от количества ПК, на которые нужно залить файл. Все бы хорошо, но он требует знания топологии сети для своей работы.
Подробнее в статье про него:
Ладно, а зачем понадобилось “гонять” 120 GiB файл по сети на такое количество ПК?
Этим файлом был VHD с операционной системой, программами, и т.п. Файл создавался на мастер‑системе, а затем распространялся на все остальные ПК. VHD был не только способом доставки системы на конечные ПК, но и давал возможность восстановления исходного состояния системы при перезагрузке ПК. Подробнее в статье: “Заморозка системы: история перехода с EWF на dVHD”.
Можно продолжить цепочку дальше, но на этом я прервусь.
Существующие протоколы обнаружения топологии канального уровня (LLDP, LLTD, CDP, …) для своей работы требуют соответствующей поддержки их со стороны всех промежуточных узлов сети. То есть они требуют как минимум управляемых свитчей, которые бы поддерживали соответствующий протокол. На Хабре уже была статья, как используя эти протоколы, “определить топологию сети на уровнях 2/3 модели OSI”.
Но что же делать, если промежуточные узлы – простые неуправляемые свитчи?
Если интересно как это можно сделать, то добро пожаловать под кат. Обещаю наличие множества иллюстраций и примеров.
Читать полностью »