Обязательно - основы теории вычислений, искусственные нейронные сети.
Желательно - генетические алгоритмы, RL-агенты.
Действительно, почему машина Тьюринга (TM) сегодня в теме про искусственный интеллект (AI) ? Ведь AI сегодня это все больше про машинное обучение (ML), искусственные нейронные сети (Читать полностью »
Научные настольные игры продолжают оставаться достаточно специализированной нишей, балансируя на грани между «обычными» настольными играми и методическими пособиями. Я решил рассказать о наиболее интересных новинках с обучающим уклоном в информатику, программирование и робототехнику, доступных в России в 2025 году.
Критерии отбора были следующие:
Игра должна быть образовательной или иметь научную тематику в части информатики, программирования или робототехники;
Игра должна быть выпущена в России или локализована на русском языке;
Мы покажем, что система, имеющая лишь команды GNU find и mkdir, полна по Тьюрингу.
Хорошо известно, что команды sed и awk сами по себе полны по Тьюрингу, но мне не удалось найти информации о Тьюринг-полноте find + mkdir.
Доказательство основано на реализации таг-системы.
Мы по порядку рассмотрим реализацию цикла, FizzBuzz и таг-системы.
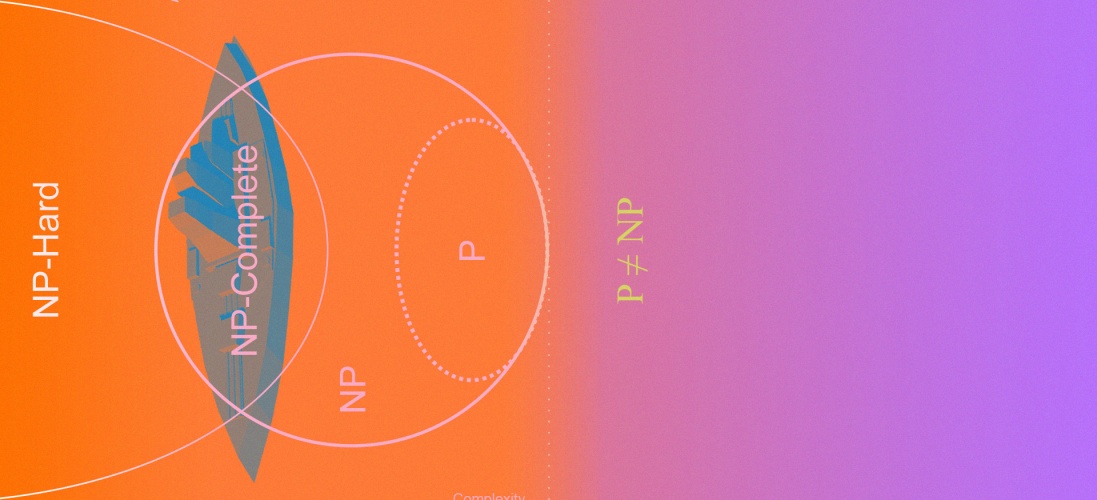
Люди часто сравнивают P и NP в таком духе, что проблемы P простые, а NP — сложные. Но это чрезмерное упрощение. На самом деле проблемы могут быть намного, намного сложнее, чем NP.
В этом смысле можно вспомнить интеллектуально-фантастический триллер Travelling Salesman (Коммивояжёр, 2012) о четырёх математиках, нанятых правительством США для решения самой сложной проблемы в истории информатики — равенства классов сложности P и NP (P versus NP problem). И им это удалось. Чиновник министерства обороны США предлагает за их алгоритм вознаграждение $10 млн. Но сами математики слишком хорошо понимают, какие разрушительные последствия принесёт в мир их открытие. Один из лучших фильмов про математику в истории кинематографа…
Читать полностью »
Привет! В свободное от работы время по вечерам мне нравится воплощать в жизнь свои сумасшедшие идеи. В один из таких вечеров родилась мысль реализовать компилятор кода в машину Тьюринга. Осознав всю тщетность бытияЧитать полностью »
DOOM (игра 1993 года для DOS) полон по Тьюрингу. Это значит, что можно запустить DOOM в DOOM. В статье приводятся подробности реализации.
Прежде чем углубляться в разработку, нужно дать немного контекста. Если вы имеете опыт программирования, то можете пропустить краткое описание понятия полноты по Тьюрингу.
Итак, какую-то видеоигру можно назвать универсальной, полной по Тьюрингу или программируемой. Что это означает? По сути, это значит, что в этой игре можно реализовать компьютер. Но тут есть свои тонкости: если для этого игроку придётся делать слишком много, то это будет уже не так интересно.
Читать полностью »
Сегодня мы отправимся в красочное путешествие по миру клеточных автоматов, попутно изучая некоторые хитрые приемы их реализации, а также попытаемся понять, что скрывается за этой красотой — любопытная игра для праздного ума или глубокая философская концепция, находящая отклики во многих моделях.
