Не одно тысячелетие математиков интересовал вопрос существования нечётных совершенных чисел. В процессе его изучения они составили невероятный список ограничений для этих гипотетических объектов. Но новые идеи на этот счёт могут появиться благодаря изучению иных близких к ним объектов.

Если нечётные совершенные числа и существуют, им придётся удовлетворять абсурдно большому списку ограничений
Будучи ещё старшеклассником, Пэйс Нильсен в середине 90-х столкнулся с математическим вопросом, над которым бьётся и по сей день. Но он не расстраивается: очаровавшая его задача, гипотеза о нечётных совершенных числах, остаётся открытой уже более 2000 лет, что делает её одной из старейших нерешённых задач математики.
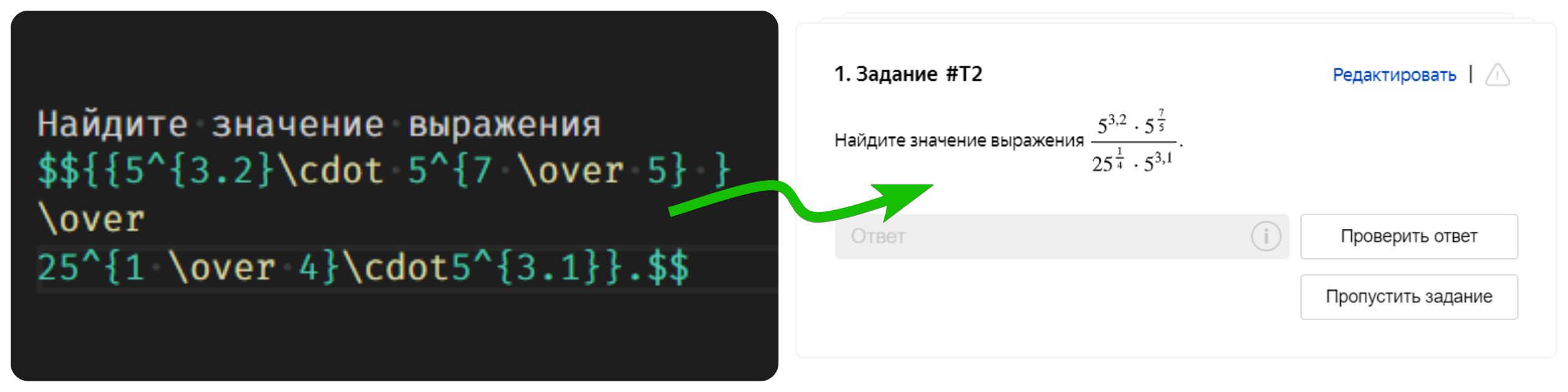
Частично таким долгоживущим шармом она обязана простоте формулировки. Число называется совершенным, если это положительное целое, n, сумма делителей которого даёт удвоенное число, 2n. Первый и самый простой пример – это 6, делители которого, 1, 2, 3 и 6, в сумме дают 12, или 2*6. Затем идёт 28, с делителями 1, 2, 4, 7, 14 и 28, дающими в сумме 56. Следующие примеры – 496 и 8128.
Читать полностью »