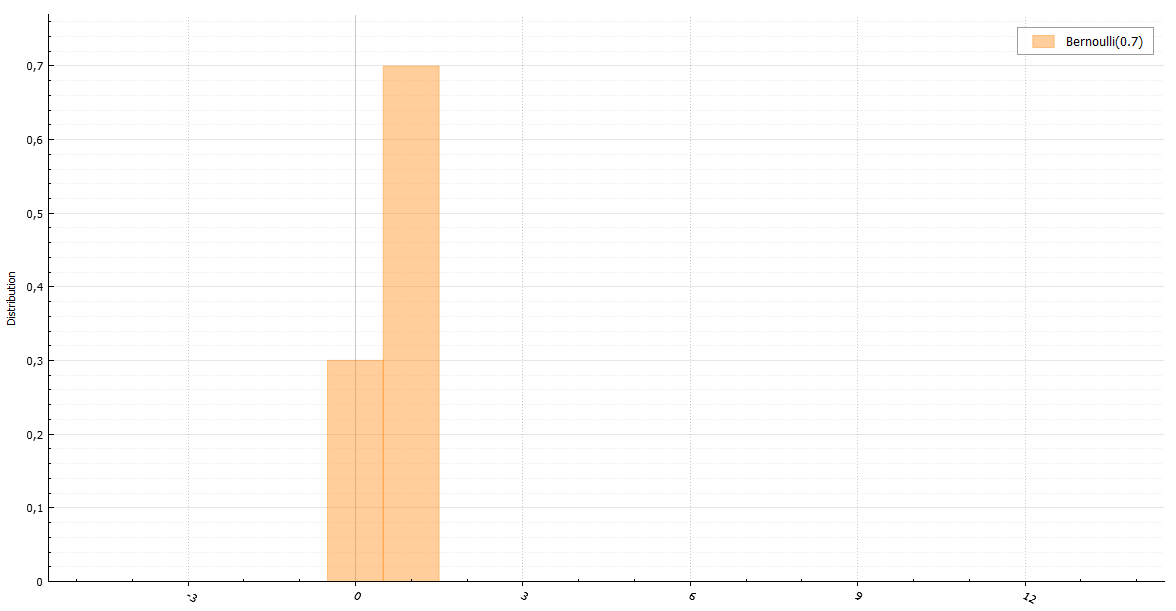Статистика приходит к нам на помощь при решении многих задач, например: когда нет возможности построить детерминированную модель, когда слишком много факторов или когда нам необходимо оценить правдоподобие построенной модели с учётом имеющихся данных. Отношение к статистике неоднозначное. Есть мнение, что существует три вида лжи: ложь, наглая ложь и статистика. С другой стороны, многие «пользователи» статистики слишком ей верят, не понимая до конца, как она работает: применяя, например, тест Стьюдента к любым данным без проверки их нормальности. Такая небрежность способна порождать серьёзные ошибки и превращать «поклонников» теста Стьюдента в ненавистников статистики. Попробуем поставить токи над i и разобраться, какие модели случайных величин должны использоваться для описания тех или иных явлений и какая между ними существует генетическая связь.
Читать полностью »
Рубрика «теория вероятностей» - 6
«Правда, чистая правда и статистика» или «15 распределений вероятности на все случаи жизни»
2016-09-30 в 7:46, admin, рубрики: f-критерий, f-распределение, f-тест, t-критерий, t-распределение, t-тест, z-критерий Фишера, z-распределение, z-тест, Алгоритмы, Анализ и проектирование систем, бета распределение, биноминальное распределение, гамма распределение, геометрическое рапределение, гипергеометрическое распределение, двойное показательное, двойное экспоненциальное, Занимательные задачки, критерий Пирсона, критерий согласия, критерий хи квадрат, математика, моделирование, нормальное распределение, отрицательное биноминальное, плотность вероятности, показательное распределение, профит фактор, распределение Бернулли, распределение Вейбулла, распределение Гаусса, распределение Коши, распределение Лапласса, распределение Паскаля, распределение Пирсона, распределение пуассона, распределение Стьюдента, распределение Фишера, распределение хи квадрат, распределение Эрланга, случайная величина, статистика, статистический тест, статитический анализ, теория вероятностей, тест Стьюдента, тест Фишера, экспоненциальное распределениеБайесовская нейронная сеть — теперь апельсиновая (часть 2)
2016-04-04 в 6:10, admin, рубрики: bayes by backprop, python, Алгоритмы, байесовский подход, математика, машинное обучение, нейронные сети, теория вероятностейКак вы думаете, чего в апельсине больше — кожуры, или, хм, апельсина?
Предлагаю, если есть возможность, пойти на кухню, взять апельсин, очистить и проверить. Если лень или нет под рукой — воспользуемся скучной математикой: объем шара мы помним из школы. Пусть, скажем, толщина кожуры равна 
Как насчет апельсина в тысячемерном пространстве?
Пойти на кухню на этот раз не получится; подозреваю, что формулу наизусть тоже не все знают, но Википедия нам в помощь. Повторяем аналогичные вычисления, и с интересом обнаруживаем, что:
- во-первых, в тысячемерном гиперапельсине кожуры больше, чем мякоти
- а во-вторых, ее больше примерно в 246993291800602563115535632700000000000000 раз
То есть, каким бы странным и противоречивым это ни казалось, но почти весь объем гиперапельсина содержится в ничтожно тонком слое прямо под его поверхностью.
Начнем с этого, пожалуй.
Байесовская нейронная сеть — потому что а почему бы и нет, черт возьми (часть 1)
2016-02-29 в 6:24, admin, рубрики: bayes by backprop, python, Алгоритмы, байесовский подход, математика, машинное обучение, теория вероятностейТо, о чем я попытаюсь сейчас рассказать, выглядит как настоящая магия.
Если вы что-то знали о нейронных сетях до этого — забудьте это и не вспоминайте, как страшный сон.
Если вы не знали ничего — вам же легче, полпути уже пройдено.
Если вы на «ты» с байесовской статистикой, читали вот эту и вот эту статьи из Deepmind — не обращайте внимания на предыдущие две строчки и разрешите потом записаться к вам на консультацию по одному богословскому вопросу.
Итак, магия:
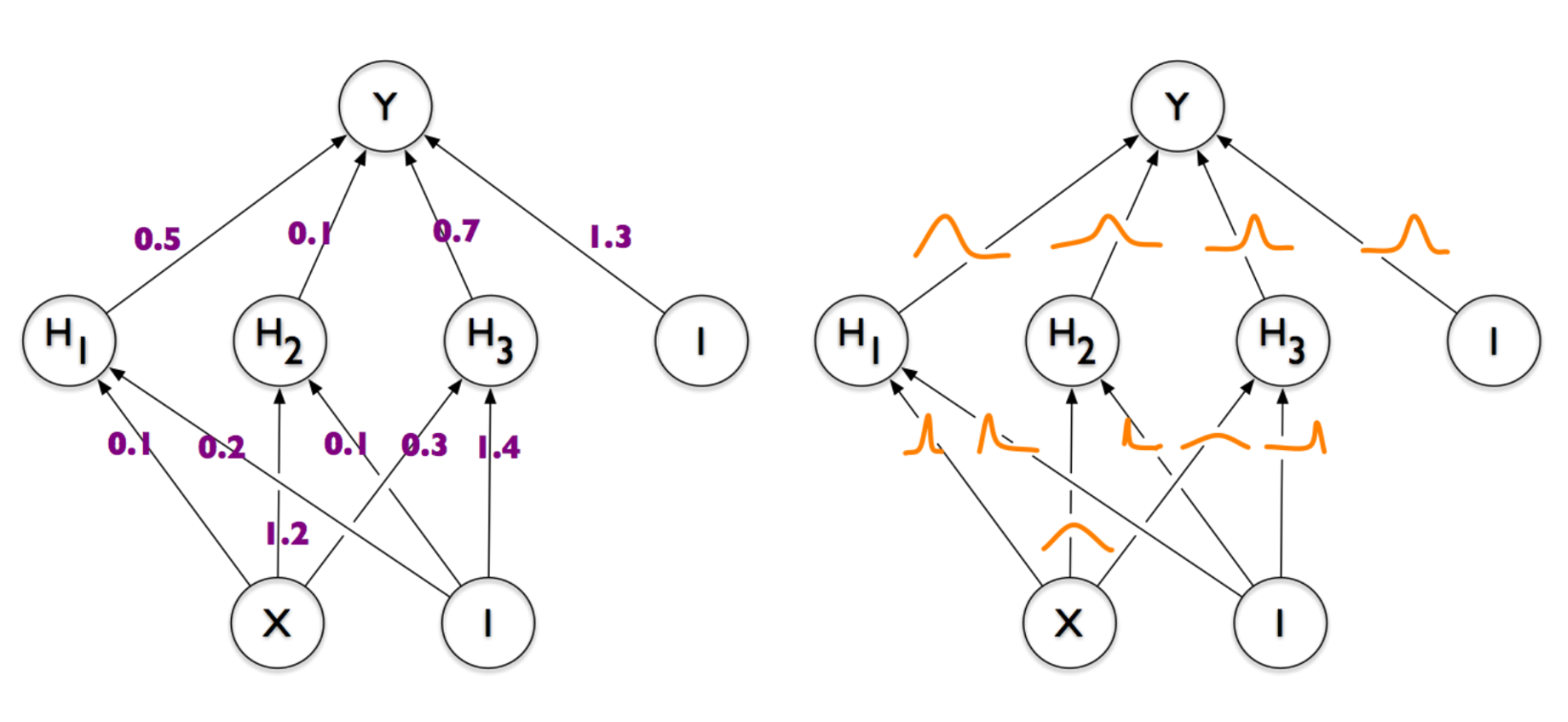
Слева — обычная и всем знакомая нейронная сеть, у которой каждая связь между парой нейронов задана каким-то числом (весом). Справа — нейронная сеть, веса которой представлены не числами, а демоническими облаками вероятности, колеблющимися всякий раз, когда дьявол играет в кости со вселенной. Именно ее мы в итоге и хотим получить. И если вы, как и я, озадаченно трясете головой и спрашиваете «а нафига все это нужно» — добро пожаловать под кат.
Зачем нужна теория вероятностей в жизни
2016-02-24 в 20:10, admin, рубрики: Блог компании Школа ясности, вебинар, всё равно никто не читает теги, Исследования и прогнозы в IT, Научно-популярное, Повышение конверсии, теория вероятностей, Учебный процесс в ITИменно под таким названием мы и провели вебинар — «Зачем нужна теория вероятностей в жизни».
В вебинаре мы не касались «жёлтых» тем типа "как выигрывать у казино" и "100% способ получить миллион без регистрации и SMS".
Наоборот, были затронуты более серьёзные. Вот сам вебинар:
Например, в индустрии статистики больше денег, чем в торговле оружием, наркотиками и людьми вместе взятыми. Один малоизвестный английский учёный в 18 веке использовал статистику длительностей жизни (так называемые актуарные таблицы, составленные ещё Галлеем, который ещё и комету Галлея открыл) и основал бизнес, который сейчас стал целой индустрией, бизнесом №1 в мире. И вы тоже в нём участвуете каждый день, сознательно или нет, например, когда едете на работу.
Идея похожего математического аппарата используется в Индии: можно купить билетик у мафии и кататься в общественном транспорте бесплатно, а полученные вами штрафы оплатит мафия. Называется «хафта» и выгодно вам и мафии, но не государству.
Генераторы дискретно распределенных случайных величин
2016-01-15 в 22:54, admin, рубрики: Алгоритмы, генераторы случайных чисел, дискретное распределение, математика, Программирование, случайная величина, случайности не случайны, теория вероятностей, метки: генераторы случайных чисел, случайная величинаДанная статья является продолжением поста Генераторы непрерывно распределенных случайных величин. В этой главе учитывается, что все теоремы из предыдущей статьи уже доказаны и генераторы, указанные в ней, уже написаны. Как и ранее, у нас имеется некий базовый генератор натуральных чисел от 0 до RAND_MAX:
unsigned long long BasicRandGenerator() {
unsigned long long randomVariable;
// some magic here
...
return randomVariable;
}
С дискретными величинами все интуитивно понятнее. Функция распределения дискретной случайной величины:
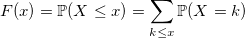
Несмотря на простоту распределений дискретных случайных величин, генерировать их подчас сложнее, нежели чем непрерывные. Начнем, как и в прошлый раз, с тривиального примера.
Распределение Бернулли
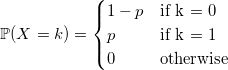
К анализу гипотезы Дрейка и парадокса Ферми
2015-11-19 в 13:37, admin, рубрики: астрономия, история, теория вероятностей, физика, физика. статистика, философия 
Многие еще со школьного курса астрономии (ну или университетского) помнят т.н. формулу Дрейка, дающая оценку количества разумных внеземных цивилизаций в нашей галактике, которая была предложена астрофизиком Френком Дрейком в 1960 году. Кстати, именно благодаря Дрейку и его формуле были выделены миллионы долларов на программу поиска внеземной жизни.
Читать полностью »
«Программирование для начинающих» + теория вероятностей
2015-10-07 в 21:17, admin, рубрики: edutainment, yasno.tv, Блог компании Школа ясности, обучение программированию, теория вероятностей, Учебный процесс в ITИнтересное дело: любой видео-курс по программированию, от PHP до Java, включает в себя главу для начинающих — чаще всего в ней рассказывается об азах структурного программирования: переменных, ветвлениях и циклах.
Поэтому мы решили раз и навсегда решить эту проблему — и сняли курс «Программирование для начинающих», который поможет самым новичкам понять и разобраться с этими базовыми понятиями, а также попробовать их в деле. Курс построен как серия видео-уроков на примере применения теории вероятностей (чтоб интереснее было).
Видео-анонс курса:
Читать полностью »
Спросите Итана №22: парадокс с отсутствием дня рождения
2015-08-11 в 22:02, admin, рубрики: спросите итана, теория вероятностей, Читальный зал 
Есть 364 дня, когда ты можешь получить подарок не на день рождения, и только один – для подарков на день рождения, знаешь ли.
— Льюис Кэрролл
Читатель спрашивает:
Среди моих 1434 фейсбучных френдов сегодня ни у кого нет дня рождения. Каковы шансы такого события, если в году 365,25 дней?
Предположим, что все ваши друзья родились после 1 марта 1900 года.
За последние 114 лет каждые 4 года случался високосный год. Предположив, что все знакомые родились в совершенно случайные дни и года, получим, что есть 4 шанса из 1461, что они родились в любой день, кроме 29 февраля, и 1 шанс из 1461, что они родились 29 февраля.
Давайте посчитаем шансы того, что у произвольного количества ваших друзей сегодня нет дня рождения. Начнём с одного.
Читать полностью »
Парадокс дней рождения для трёх человек
2015-04-21 в 14:17, admin, рубрики: Алгоритмы, математика, теория вероятностейМногим известен парадокс дней рождения: в группе из 23-х случайно отобранных людей вероятность того, что хотя бы двое из них имеют совпадающий день рождения, превышает 1/2.
Проблема, которую я буду рассматривать, сформулирована в виде упражнения в книге Алгоритмы: построение и анализ:
«Сколько нужно взять человек, чтобы с той же вероятностью 1/2 встретить хотя бы трёх с совпадающим днём рождения.»
Машинное обучение — 3. Пуассоновский случайный процесс: просмотры и клики
2015-03-25 в 7:59, admin, рубрики: Блог компании Нерепетитор.ру, Занимательные задачки, конверсия сайтов, математика, машинное обучение, Пуассон, случайные величины, случайный процесс, теория вероятностей, метки: пуассон В предыдущих статьях, посвященных вероятностному описанию конверсии сайта, мы рассматривали число событий (просмотров и кликов), как выборку случайной величины, без зависимости от времени. Теперь пришло время сделать следующий шаг и ввести ее в рассмотрение.
Читать полностью »