Этот туториал посвящён эволюционным вычислениям, тому, как они работают и как реализовать их в своих проектах и играх. После прочтения статьи вы сможете овладеть мощью эволюции для поиска решений задач, решить которые вы не можете. В качестве примера в этом туториале будет показано, как эволюционные вычисления можно использовать для обучения простого существа ходьбе. Если вы хотите ощутить мощь эволюционных вычислений в браузере, оцените Genetic Algorithm Walkers.
Читать полностью »
Часть первая — Affinity Propagation
Часть вторая — DBSCAN
Часть третья — кластеризация временных рядов
Часть четвёртая — Self-Organizing Maps (SOM)
Часть пятая — Growing Neural Gas (GNG)
Доброго времени суток! Сегодня я бы хотел рассказать об одном интересном, но крайне малоизвестном алгоритме для выделения кластеров нетипичной формы — расширяющемся нейронном газе (Growing Neural Gas, GNG). Особенно мало информации об этом инструменте анализа данных в рунете: статья в википедии, рассказ на Хабре о сильно изменённой версии GNG и пара статей с одним лишь перечислением шагов алгоритма — вот, пожалуй, и всё. Весьма странно, ведь мало какие анализаторы способны работать с меняющимися во времени распределениями и нормально воспринимают кластеры экзотической формы — а это как раз сильные стороны GNG. Под катом я попробую объяснить этот алгоритм сначала человеческим языком на простом примере, а затем более строго, в подробностях. Прошу под кат, если заинтриговал.
(На картинке: нейронный газ осторожно трогает кактус)
Читать полностью »
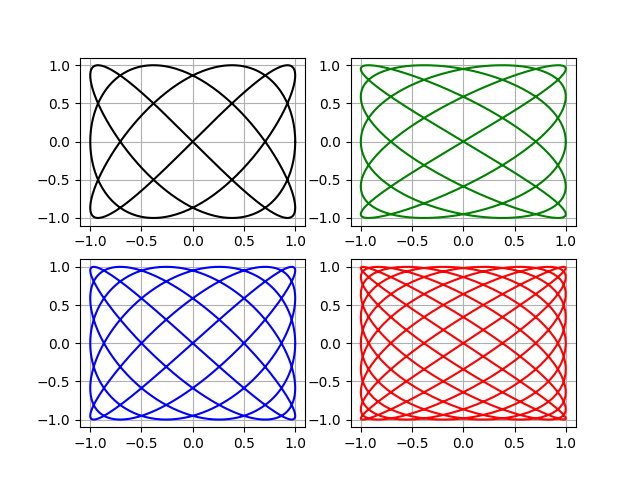
В публикации [1] подробно рассмотрена реализация на Python метода измерения отношения частот с использованием фигур Лиссажу. В качестве примера были проанализированы формы колебаний консольной эллиптической трубки вибрационного уровнемера [2].
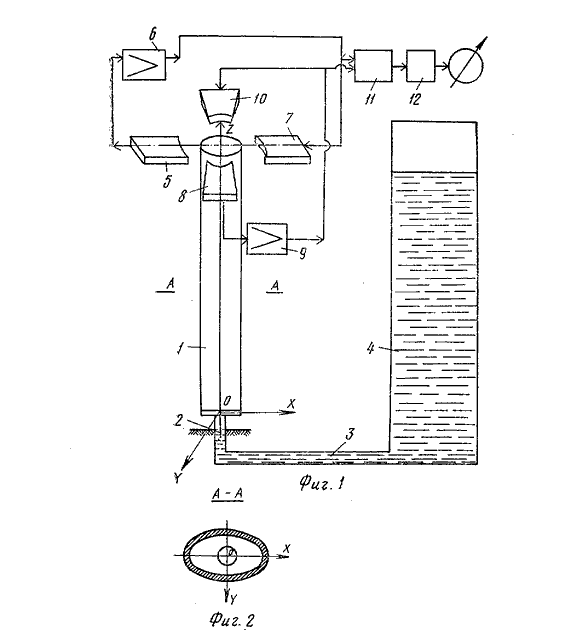
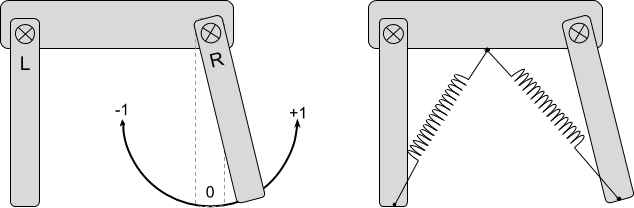
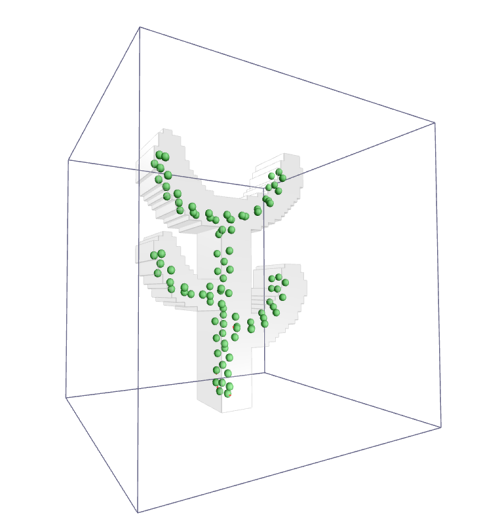
Упруго закреплённая трубка эллиптического сечения с помощью систем возбуждения 5,6,7 совершает автоколебания в одной плоскости, а с помощью систем 8, 9, 10 в другой плоскости перпендикулярной первой. Трубка колеблется в двух взаимно перпендикулярных плоскостях с разными частотами близкими к собственным. Масса трубки зависит от уровня заполняющей её жидкости.
С изменением массы меняются и частоты колебаний трубки, которые и являются выходными сигналами уровнемера. Частоты несут дополнительную информацию о мультипликативных и аддитивных дополнительных погрешностях, компенсируемых при обработке частот микропроцессором 11.
Остался не решённым вопрос определения зависимости частот колебаний трубки от уровня заполняющей жидкости что и является предметом данной публикации.
Определить частоты изгибных колебаний трубки в двух взаимно перпендикулярных плоскостях методом Релея с использованием точного уравнения изгибной линии трубки из публикации [1].
С использованием полученных соотношений для частот найти зависимости чувствительности от уровня и определить диапазоны пригодные для контроля уровня жидкости.
Для реализации указанных задач средствами Python рассмотреть два метода решения символьный и символьно-численный. Сравнить указанные методы по производительности
Читать полностью »
В этой статье рассматривается проектирование типов для работы с объектами линейной алгебры: векторами, матрицами, кватернионами. Показано классическое применение механизма перегрузки стандартных операций, использование приёма «Copy On Write» и аннотаций.
Читать полностью »
В конце сентября мы рассказывали, что решили попробовать провести контест, где желающие могут потренироваться в решении задач, максимально приближенных к «боевым». Так участники могут понять, какого формата задания получают разработчики на собеседованиях в Яндексе (этим интересуются очень многие), а самое главное — с чем они сталкиваются, работая над Поиском. Типичная задача на собеседовании — составить алгоритм, доказать его корректность, предложить пути оптимизации. Если человек разбирается в алгоритмах, то он быстро сумеет их реализовывать на любом доступном ему языке.
В Блице можно использовать Java, C++, C# или Python. Кроме того, участие в контесте дает возможность проверить свои знания. Если в итоге вы понимаете, что их стоит подтянуть, — это тоже результат. Кстати, тогда вам может пригодиться специализация на курсере «Алгоритмы и структуры данных», в создании которой Яндекс участвовал.
Давайте теперь разберем задачи, которые предлагались в отборочном раунде. У нас было несколько одинаковых по сложности вариантов, каждый из которых содержал по шесть задач. Мы разберем один набор задач полностью, а также наиболее интересные задачи из других наборов.
Яндекс уже некоторое время ведет разработку беспилотного автомобиля. Перед вами одна из первых технических лекций на эту тему. В направлении беспилотных автомобилей работают сотрудники Яндекса в разных городах, включая и Минск. Автор лекции Роман Удовиченко как раз из Минска — он руководит группой обработки дорожной ситуации. На сентябрьском Я.Субботнике Роман рассказал об одной из больших задач, стоящих перед его группой.
Мы просто берем текущее положение машины, смотрим на путь, по которому мы хотели бы ехать, и плавно сворачиваем на этот путь, выруливаем на него. Получается достаточно просто. Но перемещение в городе связано с тем, что нужно соблюдать правила дорожного движения.
Необходимым условием работоспособности системы автоматического управления (САУ), является её устойчивость. Под устойчивостью принято понимать свойство системы восстанавливать состояние равновесия, из которого она была выведена под влиянием возмущающих факторов после прекращения их воздействия [1].
Получение простого, наглядного и общедоступного инструмента для решения задач расчёта устойчивости систем автоматического управления, что является обязательным условием работоспособности любого промышленного робота и манипулятора.
Читать полностью »
Разбросаны ли простые числа по числовой оси подобно рассеянным ветром семенам? Разумеется нет: простота — это не вопрос случайности, а результат элементарной арифметики. Число является простым тогда и только тогда, когда ни одно меньшее положительное целое число кроме единицы не делит его нацело.
Но на этом история не заканчивается. Распределение простых чисел выглядит случайным, с неравномерными разрывами и скоплениями, которые выглядят довольно хаотично. Если и существует какая-то схема, то она непостижима. На самом деле, простые числа выглядят достаточно случайными, чтобы можно было сыграть с ними в кости. Создайте список последовательных простых чисел (допустим, начав с 11, 13, 17, 19,... ) и разделите их по модулю 7. Другими словами, разделите каждое простое число на 7 и сохраните только остаток. Результатом будет последовательность целых чисел из множества {1, 2, 3, 4, 5, 6}, которая выглядит почти как результат нескольких бросков правильной кости.
Особенность координатных систем на точечном базисе (ди- и би-координат) состоит в том, что их можно использовать как в обычном геометрическом пространстве, так и в пространстве графа.
Пространство графа — это множество связанных между собой узлов (вершин графа). Каждый узел графа — это точка его пространства. В отличие от обычного геометрического пространства мерность пространства графа определяется количеством его узлов, — чем их больше, тем больше мерность.
Задачу построения системы координат (СК) на графе можно сформулировать следующим образом.
Читать полностью »
С появлением библиотеки SymPy для решения математических задач появились дополнительные возможности, позволяющие отображать результаты в символьной форме.
Подробное описание использования символьных вычислений приведено в публикации [1] под названием «Введение в научный Python» в разделе «Символьные вычисления».
Расширение области применения символьных вычислений на решение отдельных задач нелинейного программирования надеюсь будет способствовать популяризации Python в том числе и как альтернатива дорогостоящих математических пакетов.
Привести примеры символьных вычислений для безусловного экстремума дифференцируемой нелинейной функции цели с определением достаточных условий существования экстремума по матрице Гессе. Рассмотреть так же задачу условного нелинейного программирования с линейными ограничениями при помощи множетелей Лагранжа.
Для того, чтобы определиться с терминологией приведу следующее определение [2]. Задачей нелинейного программирования (задачей НП) называется задача нахождения максимума (минимума) нелинейной функции многих переменных, когда на переменные имеются (не имеются) ограничения типа равенств или неравенств.
Несмотря на сложность решаемых задач при символьном решении всё становится простым и наглядным. Рассмотрим листинг первого примера.Читать полностью »
