В детстве каждое лето я проводил на даче. Наша дача находилась довольно далеко от Ленинграда в небольшом посёлке со старинным финским названием. Рядом были красивые озера и заповедные леса. У моих дедушки с бабушкой был небольшой вытянутый участок на горе с ветхими, но аккуратными деревянными постройками и высокими стройными соснами. Из города до дачи мы с добирались на пригородном автобусе или на электричке. На автобусе было даже удобнее — прямо за нашим дачным забором проходило шоссе и была расположена автобусная остановка.
Рубрика «комбинаторика»
Счастливые автобусные билетики — магия чисел для советских школьников
2026-01-08 в 20:58, admin, рубрики: автобус, детство, журнал квант, коллекция, комбинаторика, ленинград, ностальгия, СССР, счастливые билетики, счастливые билетыГайд по техникам тест-дизайна: нюансы и механики. Часть 1
2025-06-17 в 7:00, admin, рубрики: гайд, комбинаторика, Ланит, методики тест-дизайна, обучение, советы, сценарии тестирования, тест-дизайн, тестирование, эффективностьТестирование программного обеспечения уже давно сопровождает процесс разработки в ru-сегменте. Для новичков, и не только, часто остается не до конца раскрытым процесс тест-дизайна. Курсы и статьи дают информацию о техниках разного уровня описания, полноты и качества.
Как Выигрывать в Игре Быки и Коровы
2024-09-09 в 20:57, admin, рубрики: Gamedev, mastermind, быки и коровы, комбинаторикаСуществует старинная народная логическая игра. Называется быки и коровы. Её ещё называют mastermind.

Правила простые:
Получаем деньги за подбрасывание монет стоимостью в миллионы долларов
2024-03-02 в 7:57, admin, рубрики: комбинаторикаБезотказный способ вовлечь людей в дискуссию — регулярно публиковать эту штуку в Twitter. Иногда я ненавижу подобные скрупулёзные разборы тем, но в данном случае, к чёрту, давайте разберём эту хреновину по косточкам, и посмотрим, сколько полезной информации мы можем из неё извлечь.
Ответом на задачу по упаковке цветов в бесконечной сетке оказалось число 15
2023-04-28 в 13:00, admin, рубрики: infinite grid, ruvds_перевод, Алгоритмы, алгоритмы поиска, бесконечная сетка, Блог компании RUVDS.com, графы, комбинаторика, математика
В задаче по «упаковке цветов графа» (в оригинале packing coloring, — прим. пер.) спрашивается, сколько чисел необходимо для заполнения бесконечной сетки так, чтобы идентичные числа никогда не оказывались слишком близко друг к другу. И новый арифметический эксперимент с использованием компьютера даёт на удивление простой ответ.
Сколько чисел потребуется для заполнения бесконечной сетки так, чтобы расстояние между вхождениями одного числа было больше самого этого числа?Читать полностью »
Игра «Жизнь» — как собрать произвольный шаблон всего из 15 глайдеров
2023-01-21 в 9:09, admin, рубрики: life, Игры и игровые консоли, исследование, комбинаторика, математика, Научно-популярное, ПрограммированиеВ сообществе игры «Жизнь», изобретённой Джоном Конвеем, отмечали знаковое достижение, совершённое 9 ноября 2022 года. Идея, на воплощение которой ушли годы – проект «обратный шестометатель» — наконец дошла до той стадии, когда в наличии имелись все компоненты для этой сущности, позволявшие достичь заявленной цели.
Цель проста. Выбираем любой шаблон, который можно собрать в «Жизни» - например, ТихоходкуЧитать полностью »
Задача про две ёмкости для жидкости
2022-04-23 в 14:05, admin, рубрики: dot, FSM, GraphViz, svg, Графические оболочки, динамическое программирование, дискретная математика, интервью, комбинаторика, логические игры, математика, Программирование, собеседование в IT, собеседованияСуществует классическая задача:
Есть 2 емкости: 5 литров и 3 литра. Как отмерить 4 литра жидкости используя только эти 2 емкости?
Понятное дело что тут важно не сколько знание правильного ответа, а знание метода решения таких задач. Ведь вместо целевых 4х литров могут спросить отсчитать и 1,2,6,7 литров.
В этом тексте я решу эту задачу в общем виде при помощи конечного автомата. Так как тут явно можно проследить состояния и входные воздействия. Также я упомяну про малоизвестный язык Front-End разметки DotЧитать полностью »
Как на Python подобрать экипировку для игрового перса
2020-04-05 в 15:23, admin, рубрики: python, rpg, world of warcraft, анализ, игры, Игры и игровые приставки, комбинаторикаУчимся находить лучшее для своего разбойника при помощи программирования. Также разбираемся, не водит ли нас программа «за нос».
Открытые онлайн-материалы от Computer Science центра, часть 2
2020-03-31 в 15:47, admin, рубрики: cs центр, Go, latex, Rust, stan, Блог компании Образовательные проекты JetBrains, видеокурсы, комбинаторика, математика, операционные системы, открытые лекции, ПрограммированиеВ первой части поста мы рассказали о наших популярных онлайн-курсах на Stepik, а теперь выкладываем записи открытых лекций и видеокурсов на YouTube и напоминаем о том, что до 11 апреля открыт новый набор в CS центр в Санкт-Петербурге и Новосибирске.
Элемент нулевого размера
2019-06-16 в 9:18, admin, рубрики: Анализ и проектирование систем, графы, изобретение, инженерные системы, комбинаторика, Научно-популярное, проектирование, ТРИЗ, функция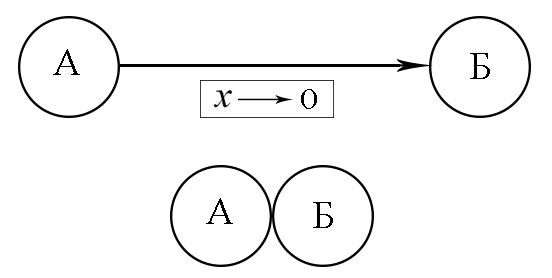
Графы — схематическое обозначение во многих сферах.
Модель реальных объектов.
Круги — вершины, линии — дуги графа (соединения).
Если рядом с дугой цифра — это расстояние между точками на карте или стоимость на диаграмме Ганта.
В электрике и электронике вершины — это детали и модули, линии — проводники.
В гидравлике котлы, бойлеры, арматура, радиаторы и трубы.
На карте — города и дороги.
Из школьной задачи по математике:
Из пункта А в пункт Б выехал автобус. Расстояние между пунктами 30 км.
А что если расстояние 0?
Читать полностью »